
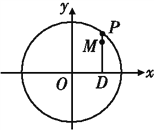
【题目】如图,设P是圆![]() 上的动点,点D是P在x轴上的投影,M为线段PD上一点,且
上的动点,点D是P在x轴上的投影,M为线段PD上一点,且![]() ,
,
(1)当P在圆上运动时,求点M的轨迹C的方程;
(2)求过点(3,0)且斜率为![]() 的直线被轨迹C所截线段的长度.
的直线被轨迹C所截线段的长度.
科目:高中数学 来源: 题型:
【题目】漳州市博物馆为了保护一件珍贵文物,需要在馆内一种透明又密封的长方体玻璃保护罩内充入保护液体.该博物馆需要支付的总费用由两部分组成:①罩内该种液体的体积比保护罩的容积少0.5立方米,且每立方米液体费用500元;②需支付一定的保险费用,且支付的保险费用与保护罩容积成反比,当容积为2立方米时,支付的保险费用为4000元.
(Ⅰ)求该博物馆支付总费用![]() 与保护罩容积
与保护罩容积![]() 之间的函数关系式;
之间的函数关系式;
(Ⅱ)求该博物馆支付总费用的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() ,判断函数
,判断函数![]() 的单调性;
的单调性;
(2)若函数![]() 在定义域内单调递减,求实数
在定义域内单调递减,求实数![]() 的取值范围;
的取值范围;
(3)当![]() 时,关于
时,关于![]() 的方程
的方程![]() 在
在![]() 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
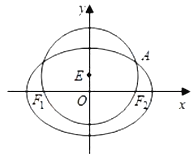
【题目】已知圆![]() :
: ![]() 经过椭圆
经过椭圆![]() :
: ![]() 的左右焦点
的左右焦点![]() ,且与椭圆
,且与椭圆![]() 在第一象限的交点为
在第一象限的交点为![]() ,且
,且![]() 三点共线,直线
三点共线,直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
, ![]() 两点,且
两点,且![]() (
(![]() ).
).
(1)求椭圆![]() 的方程;
的方程;
(2)当三角形![]() 的面积取得最大值时,求直线
的面积取得最大值时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象如图所示.
的图象如图所示.

(Ⅰ)求![]() 的值;
的值;
(Ⅱ)若函数![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,求函数
,求函数![]() 的解析式;
的解析式;
(Ⅲ)在(Ⅱ)的条件下,函数![]() 与
与![]() 的图象有三个不同的交点,求
的图象有三个不同的交点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com