
曲线x2﹣y2=1经过伸缩变换T得到曲线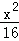 ﹣
﹣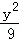 =1,那么直线x﹣2y+1=0经过伸缩变换T得到的直线方程为( )
=1,那么直线x﹣2y+1=0经过伸缩变换T得到的直线方程为( )
A.2x﹣3y+6=0 B.4x﹣6y+1=0 C.3x﹣8y+12=0 D.3x﹣8y+1=0
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:[同步]2014年新人教A版选修4-2 2.1复合变换与二阶矩阵的乘法(解析版) 题型:解答题
已知矩阵M=[ ]N=[
]N=[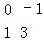 ].
].
(1)求矩阵MN;
(2)若点P在矩阵MN对应的变换作用下得到Q(0,1),求点P的坐标.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-2 1.2二阶矩阵与平面向量的乘法(解析版) 题型:选择题
定义运算 ,如
,如 ,已知α+β=π,
,已知α+β=π,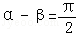 ,则
,则 =( )
=( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-2 1.1线性变换与二阶矩阵练习卷(解析版) 题型:填空题
(2013•石家庄二模)将函数y=﹣x2+x(e∈[0,1])的图象绕点M(1,0)顺时针旋转θ角 (0<θ< )得到曲线C,若曲线C仍是一个函数的图象,则角θ的最大值为 .
)得到曲线C,若曲线C仍是一个函数的图象,则角θ的最大值为 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-2 1.1线性变换与二阶矩阵练习卷(解析版) 题型:选择题
在平面直角坐标系中O为坐标原点,P(3,4),将向量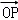 绕原点顺时针方向旋转
绕原点顺时针方向旋转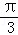 ,并将其长度伸长为原来的2倍的向量
,并将其长度伸长为原来的2倍的向量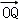 ,则点Q的坐标是( )
,则点Q的坐标是( )
A.(3+4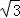 ,4﹣3
,4﹣3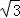 ) B.(4+3
) B.(4+3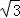 ,4﹣3
,4﹣3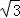 )
)
C.(3+4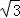 ,3
,3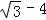 ) D.(3﹣4
) D.(3﹣4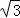 ,3﹣4
,3﹣4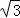 )
)
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-2 1.1线性变换与二阶矩阵练习卷(解析版) 题型:选择题
将直线y=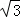 x绕原点逆时针旋转60°,所得到的直线为( )
x绕原点逆时针旋转60°,所得到的直线为( )
A.x=0 B.y=0 C.y=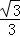 x D.y=﹣
x D.y=﹣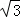 x
x
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 3.3平面与圆锥面的截线练习卷(解析版) 题型:填空题
(2007•茂名二模)已知圆柱半径是2,则是一个与圆柱的轴成45°角的平面截圆柱面所得截痕曲线的离心率是 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 3.1平行射影练习卷(解析版) 题型:填空题
给出下列四个命题:
①设x1,x2∈R,则x1>1且x2>1的充要条件是x1+x2>2且x1x2>1;
②任意的锐角三角形ABC中,有sinA>cosB成立;
③平面上n个圆最多将平面分成2n2﹣4n+4个部分;
④空间中直角在一个平面上的正投影可以是钝角.
其中真命题的序号是 (要求写出所有真命题的序号).
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 2.1圆周角定理练习卷(解析版) 题型:填空题
(2013•惠州二模)(几何证明选讲选做题)
如图所示,AB是圆O的直径, ,AB=10,BD=8,则cos∠BCE= .
,AB=10,BD=8,则cos∠BCE= .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com