
| 分组(身高) | [125,130) | [130,135) | [135,140) | [140,145] |
分析 (Ⅰ)按照分层抽样的方法按比例求出身高在[125,130)的女生应抽取几人;
(Ⅱ)在(Ⅰ)中抽取的6名女生中,有4人身高在[125,130)中,2人身高在[140,145]中,问题为古典概型,列举基本事件,即可求出概率.
解答 解:(Ⅰ)身高在[125,130)内的女生应该抽取$\frac{20}{20+10}×6=4$人.
(Ⅱ)在(Ⅰ)中抽取的6名女生中,有4人身高在[125,130)中,2人身高在[140,145]中,记身高在[125,130)中的4人分别为a,b,c,d,身高在[140,145]中的2人分别为A,B.从这6人中随机抽取2人,基本事件包含(a,b),(a,c),(a,d),(a,A),(a,B),(b,c),(b,d),(b,A),(b,B),(c,d),(c,A),(c,B),(d,A),(d,B),(A,B),共有15个基本事件.
其中2人身高都在[125,130)内的情况有6种,
则2人身高都在[125,130)内的概率为$P=\frac{6}{15}=\frac{2}{5}$.
点评 本题考查频率分布直方图的基础知识,分层抽样,古典概型求解.融合了基本知识,难度不大,但是好题.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $4\sqrt{3}$ | B. | 4 | C. | -4$\sqrt{3}$ | D. | -4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
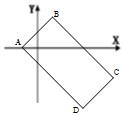 如图,已知复平面内平行四边形ABCD中,点A对应的复数为-1,$\overrightarrow{AB}$对应的复数为2+2i,$\overrightarrow{BC}$对应的复数为4-4i.
如图,已知复平面内平行四边形ABCD中,点A对应的复数为-1,$\overrightarrow{AB}$对应的复数为2+2i,$\overrightarrow{BC}$对应的复数为4-4i.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 推理一般分为合情推理和演绎推理 | |
| B. | 归纳是从特殊到一般的过程,它属于合情推理 | |
| C. | 在数学中,证明命题的正确性既能用演绎推理又能用合情推理 | |
| D. | 演绎推理经常使用的是由大前提、小前提得到结论的三段论推理 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 推理形式错误 | B. | 大前提错误 | ||
| C. | 小前提错误 | D. | 大前提和小前提都错误 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2017}{2}$ | B. | 2017 | C. | $\frac{2018}{2}$ | D. | 2018 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com