
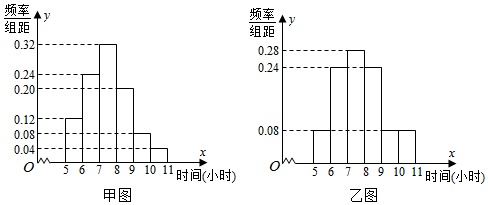
分析 (Ⅰ)由频率分布直方图能求出两所学校被抽取到的学生每周用于体育锻炼时间的平均数.
(Ⅱ)每周体育锻炼时间不低于10个小时的学生中,甲校有2人,乙校有4人,X的所有可能取值有1,2,3,分别求出相应的概率,由此能求出X的分布列和EX.
解答 解:(Ⅰ)由频率分布直方图得甲校被抽取到的学生每周用于体育锻炼时间的平均数为:
$\overline{{x}_{甲}}$=0.12×5.5+0.24×6.5+0.32×7.5+0.20×8.5+0.08×9.5+0.04×10.5=7.5.
乙校被抽取到的学生每周用于体育锻炼时间的平均数为:
$\overline{{x}_{乙}}$=0.08×5.5+0.24×6.5+0.28×7.5+0.24×8.5+0.08×9.5+0.08×10.5=7.74.
(Ⅱ)每周体育锻炼时间不低于10个小时的学生中,甲校有2人,乙校有4人,
X的所有可能取值有1,2,3,
P(X=1)=$\frac{{C}_{2}^{2}{C}_{4}^{1}}{{C}_{6}^{3}}$=$\frac{1}{5}$,
P(X=2)=$\frac{{C}_{2}^{1}{C}_{4}^{2}}{{C}_{6}^{3}}$=$\frac{3}{5}$,
P(X=3)=$\frac{{C}_{2}^{0}{C}_{4}^{3}}{{C}_{6}^{3}}$=$\frac{1}{5}$,
∴X的分布列为:
| X | 1 | 2 | 3 |
| P | $\frac{1}{5}$ | $\frac{3}{5}$ | $\frac{1}{5}$ |
点评 本题考查平均数的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意频率分布直方图的性质的合理运用.


 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | -$\frac{1}{5}$ | D. | $\frac{2}{5}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
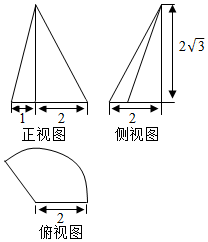 某几何体的三视图如图所示,其中俯视图为扇形,则一个质点从扇形的圆心起始,绕几何体的侧面运动一周回到起点,其最短路径为( )
某几何体的三视图如图所示,其中俯视图为扇形,则一个质点从扇形的圆心起始,绕几何体的侧面运动一周回到起点,其最短路径为( )| A. | 4+$\frac{4π}{3}$ | B. | 6$\sqrt{3}$ | C. | 4+$\frac{2π}{3}$ | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-5<x<3} | B. | {x|-4<x<2} | C. | {x|-4<x<5} | D. | {x|-2<x<3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-4,1] | B. | [-4,1) | C. | (-2,1] | D. | [-2,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
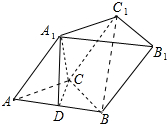 如图,三棱柱ABC-A1B1C1中,A1C⊥底面ABC,∠ACB=120°,A1C=AC=BC=2,D为AB中点.
如图,三棱柱ABC-A1B1C1中,A1C⊥底面ABC,∠ACB=120°,A1C=AC=BC=2,D为AB中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com