
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{4}$ |
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| t(时) | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y(米) | 1.41 | 0.88 | 0.39 | 0.91 | 1.38 | 0.90 | 0.42 | 0.89 | 1.40 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
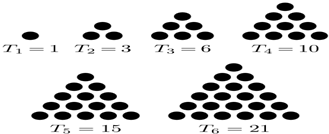 小毕喜欢把数描绘成沙滩上的小石子,他照如图所示摆成了正三角形图案,并把每个图案中总的石子个数叫做“三角形数”,记为Tn,则$\frac{1}{2{T}_{1}}$+$\frac{1}{2{T}_{2}}$+$\frac{1}{2{T}_{3}}$+…+$\frac{1}{2{T}_{2015}}$=$\frac{2015}{2016}$.
小毕喜欢把数描绘成沙滩上的小石子,他照如图所示摆成了正三角形图案,并把每个图案中总的石子个数叫做“三角形数”,记为Tn,则$\frac{1}{2{T}_{1}}$+$\frac{1}{2{T}_{2}}$+$\frac{1}{2{T}_{3}}$+…+$\frac{1}{2{T}_{2015}}$=$\frac{2015}{2016}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com