练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    14．将一个四棱锥的每一个顶点染上一种颜色，并使同一条棱上的两端异色，如果只有5种颜色可供使用，有420种染色方法．

    分析 首先给顶点P选色，有5种结果，再给A选色有4种结果，再给B选色有3种结果，最后分两种情况即B与D同色、B与D不同色来讨论，根据分步计数原理和分类计数原理得到结果．

    解答 解：设四棱锥为P-ABCD．
    下面分两种情况即B与D同色与B与D不同色来讨论，
    （1）P：C51，A：C41，B：C31，
    B与D同色：D：1，C：C31．
    （2）P：C51，A：C41，B：C31，
    B与D不同色：D：C21，C：C21．
    共有C51•C41•C31•1•C31+C51•C41•C31•C21•C21=420．
    故答案为：420

    点评 本题主要排列与组合及两个基本原理，总体需分类，每类再分步，综合利用两个原理解决，属中档题

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    4．下面四个命题：
    ①有一段演绎推理“有些有理数是真分数，整数是有理数，则整数是真分数”，结论显然错误，是因为大前提错误；
    ②在两个变量y与x的回归模型中，分别选择了四个不同的模型，它们的相关指数R2分别为：（1）0.976；（2）0.776，（3）0.076；（4）0.351，其中拟合效果最好的模型是（1）；
    ③设a，b，c∈（-∞，0），则a+$\frac{1}{b}$，b+$\frac{1}{c}$，c+$\frac{1}{a}$至少有一个不大于-2；
    ④如果一个直角三角形的两条边长分别是6和8，另一个与它相似的直角三角形边长分别是3和4及x，那么x的值是5．
    其中所有正确命题的序号是②③．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．圆（x-1）2+（y+2）2=6与直线2x+y-5=0的位置关系是（　　）
    A．相切B．相交但直线不过圆心
    C．相交且过圆心D．相离

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．对于三次函数f（x）=ax3+bx2+cx+d（a≠0），给出定义：f′（x）是函数f（x）的导函数，f″（x）是f′（x）的导函数，若方程f″（x）=0有实数解x0，则称点（x0，f（x0））为函数y=f（x）的“拐点”．某同学经研究发现：任何一个三次函数都有“拐点”；任何一个三次函数都有对称中心，且“拐点”就是对称中心．若f（x）=$\frac{1}{3}$x3-$\frac{1}{2}$x2+3x-$\frac{5}{12}$，根据这一发现，可求得f（$\frac{1}{2016}$）+f（$\frac{2}{2016}$）+…+f（$\frac{2015}{2016}$）=2015．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．从甲地到乙地一天有汽车8班，火车3班，轮船2班，某人从甲地到乙地，他共有不同的走法数为（　　）
    A．48种B．16种C．24种D．13种

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．函数f（x）=lnx+$\frac{1}{x}$+ax（a∈R）
    （1）a=0时，求f（x）最小值；
    （2）若f（x）在[2，+∞）是单调减函数，求a取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．函数f（x）=$\sqrt{3-2x-{x}^{2}}$的定义域为[-3，1]，值域为[0，2]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．若函数f（x）=sin（ωx+θ）的图象（部分）如图所示，则ω和θ的取值是（　　）
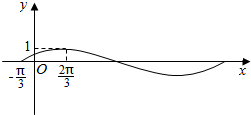
    A．$ω=1，θ=\frac{π}{3}$B．$ω=1，θ=-\frac{π}{3}$C．$ω=\frac{1}{2}，θ=\frac{π}{6}$D．$ω=\frac{1}{2}，θ=-\frac{π}{6}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．若f（x）=x3-ax+1在（0，1）上单调递减，则实数a的取值范围是（　　）
    A．a≤2B．a≤3C．a＞3D．a≥3

    查看答案和解析>>

    同步练习册答案