
分析 (1)由数列的前n项和求出首项和n≥2时的通项,结合数列为等比数列可知首项符合n≥2时的通项,由此求得a值,并进一步求得{an}的通项公式;
(2)把数列{an}的通项公式代入bn=$\frac{1}{n}(log_2{a_1}+log_2{a_2}+…+log_2{a_n})$,利用对数的运算性质及等差数列的前n项和求得bn,代入数列$\left\{{\frac{1}{{{b_n}•{b_{n+1}}}}}\right\}$,然后利用裂项相消法求得数列$\left\{{\frac{1}{{{b_n}•{b_{n+1}}}}}\right\}$的前n项和;
(3)利用作差法可得$\left\{{\frac{a_n}{b_n}}\right\}$在其定义域上单调递增,由此求得数列$\left\{{\frac{a_n}{b_n}}\right\}$的最小项的值.
解答 解:(1)∵${S_n}={2^{n+6}}-a$,
∴${a}_{1}={S}_{1}={2}^{7}-a$,
当n≥2时,${S_{n-1}}={2^{n+5}}-a$,
∴${a_n}={S_n}-{S_{n-1}}={2^{n+5}}$,
∵数列{an}是等比数列,
∴${a}_{1}={2}^{6}={2}^{7}-a$,解得a=64.
∴${a_n}={2^{n+5}}$;
(2)bn=$\frac{1}{n}(log_2{a_1}+log_2{a_2}+…+log_2{a_n})$
=$\frac{1}{n}(1+2+3+…+n+5n)$=$\frac{1}{n}•[\frac{n(n+1)}{2}+5n]$=$\frac{n+11}{2}$,
$\frac{1}{{{b_n}{b_{n+1}}}}=\frac{4}{(n+11)(n+12)}=4(\frac{1}{n+11}-\frac{1}{n+12})$,
∴${T_n}=4(\frac{1}{12}-\frac{1}{13}+\frac{1}{13}-\frac{1}{14}+…+\frac{1}{n+11}-\frac{1}{n+12})$
=$4(\frac{1}{12}-\frac{1}{n+12})$;
(3)∵${a}_{n}={2}^{n+5}$,bn=$\frac{n+11}{2}$,
∴$\frac{{a}_{n}}{{b}_{n}}=\frac{{2}^{n+5}}{\frac{n+11}{2}}=\frac{{2}^{n+6}}{n+11}$,
则$\frac{{a}_{n+1}}{{b}_{n+1}}-\frac{{a}_{n}}{{b}_{n}}=\frac{{2}^{n+7}}{n+12}-\frac{{2}^{n+6}}{n+11}=\frac{{2}^{n+7}(n+11)-{2}^{n+6}(n+12)}{(n+12)(n+11)}$
=$\frac{{{2^{n+6}}[{({2n+22})-(n+12)}]}}{{(n+12)({n+11})}}$=$\frac{{{2^{n+6}}({n+10})}}{{(n+12)({n+11})}}>0$,
∴$\left\{{\frac{a_n}{b_n}}\right\}$在其定义域上单调递增.
∴$\left\{{\frac{a_n}{b_n}}\right\}$min=$\frac{a_1}{b_1}$=$\frac{32}{3}$.
点评 本题考查数列递推式,考查了等比关系的确定,训练了裂项相消法求数列的前n项和,考查了数列的函数特性,是中档题.


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,π] | B. | [-$\frac{π}{3}$,$\frac{2π}{3}$] | C. | [-$\frac{π}{6}$,$\frac{7π}{6}$] | D. | [-$\frac{π}{3}$,$\frac{4π}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 6 | 8 | 10 | 12 |
| y | 2 | 3 | 5 | 6 |
| A. | 1.2 | B. | -1.2 | C. | -2.3 | D. | 7.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
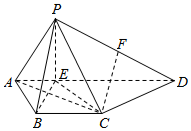 如图所示的几何体P-ABCD中,底面ABCD是梯形,且AD∥BC,点E是边AD上的一点,AE=BC=AB,AD=3BC,点F是PD的中点,PB⊥AC.
如图所示的几何体P-ABCD中,底面ABCD是梯形,且AD∥BC,点E是边AD上的一点,AE=BC=AB,AD=3BC,点F是PD的中点,PB⊥AC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2,4 | B. | 4,4 | C. | 2,0 | D. | 4,2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com