
| A. | (-∞,4] | B. | [-4,4] | C. | [-2,4] | D. | [-1,4] |
分析 把已知的等式变形,得到2a2+2b2+8c2=8,然后结合基本不等式求得ab+2bc+2ca≤4;再由($\frac{1}{2}$a+$\frac{1}{2}$b+c)2≥0,结合已知的等式求得ab+2bc+2ca≥-2.
解答 解:由$\frac{1}{4}$a2+$\frac{1}{4}$b2+c2=1,得a2+b2+4c2=4,即2a2+2b2+8c2=8.
∴8=2a2+2b2+8c2=(a2+b2)+(a2+4c2)+(b2+4c2)≥2ab+4ac+4bc.
∴ab+2bc+2ca≤4(当且仅当a=b=2c时取等号);
又$\frac{1}{4}$a2+$\frac{1}{4}$b2+c2+2($\frac{1}{4}$ab+$\frac{1}{2}$bc+$\frac{1}{2}$ca)=($\frac{1}{2}$a+$\frac{1}{2}$b+c)2≥0,
∴1+$\frac{1}{2}$(ab+2bc+2ca)≥0,
∴ab+2bc+2ca≥-2.
则ab+2bc+2ca的取值范围是[-2,4].
故选:C.
点评 本题考查基本不等式求最值,考查了灵活变形能力,是中档题.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 10 | C. | 15 | D. | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 总体 | B. | 个体是每一个零件 | ||
| C. | 总体的一个样本 | D. | 样本容量 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| X | -2 | -1 | 0 | 1 | 2 |
| P | $\frac{1}{4}$ | $\frac{1}{3}$ | $\frac{1}{5}$ | m | $\frac{1}{20}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
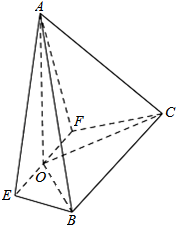 如图,在四棱锥A-EFCB中,△AEF为等边三角形,平面AEF⊥平面EFCB,EF∥BC,BC=4,EF=2a,∠EBC=∠FCB=60°,O为EF的中点.
如图,在四棱锥A-EFCB中,△AEF为等边三角形,平面AEF⊥平面EFCB,EF∥BC,BC=4,EF=2a,∠EBC=∠FCB=60°,O为EF的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com