
分析 (1)把4×6n+5n+1-9=4•(5+1)n+5•(4+1)n-9按照二项式定理展开,提取公因式,可得结论成立.
(2)利用二项式定理把 3100=(7+2)50按照二项式定理展开,化简为7Mn+250(Mn∈N+),再把250 =4(1+7)16按照二项式定理展开,可得3100被7除余数,从而得出结论.
解答 (1)证明:∵4×6n+5n+1-9=4•(5+1)n+5•(4+1)n-9
=4(Cn05n+Cn15n-1+…+Cnn-15+1)+5(Cn04n+Cn14n-1+…+Cnn-14+1)-9
=20[(Cn05n-1+Cn15n-2+…+Cnn-1)+(Cn04n-1+Cn14n-2+…+Cnn-1)],
故结论成立.
(2)解:设7Mn表示7和一个正整数的乘积,
∵3100=950=(7+2)50=C500•750•20+C501•749•21+…+C5049•7•249+C5050•70•250
=7Mn+250(Mn∈N+),
又250=23×16+2=4×816=4(1+7)16=4(C160+7C161+72C162+…+716C1616)=4+7Nn(Nn∈N+),
∴3100被7除余数是4,故再过3100天是星期五.
点评 本题主要考查二项式定理的应用,属于中档题.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:填空题
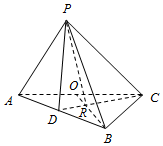 在三棱锥P-ABC中,AB⊥BC,AB=6,$BC=2\sqrt{3}$,O为AC的中点,过C作BO的垂线,交BO、AB分别于R、D.若∠DPR=∠CPR,则三棱锥P-ABC体积的最大值为3$\sqrt{3}$.
在三棱锥P-ABC中,AB⊥BC,AB=6,$BC=2\sqrt{3}$,O为AC的中点,过C作BO的垂线,交BO、AB分别于R、D.若∠DPR=∠CPR,则三棱锥P-ABC体积的最大值为3$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,3) | B. | (-1,2) | C. | (1,3) | D. | (2,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 选修课程 | 线性代数 | 微积分 | 大学物理 | 商务英语 | 文学写作 | 合计 |
| 选课人数 | 180 | x | 120 | y | 60 | 600 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
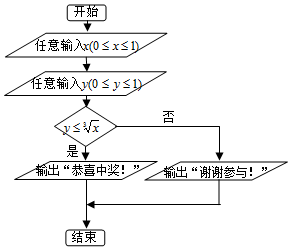 在如图的程序框图中,任意输入一次x(0≤x≤1)与y(0≤y≤1),则能输出“恭喜中奖!”的概率为( )
在如图的程序框图中,任意输入一次x(0≤x≤1)与y(0≤y≤1),则能输出“恭喜中奖!”的概率为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “am2<bm2”是“a<b”的充分不必要条件 | |
| B. | 命题“?x∈R,x3-x2-1≤0”的否定是“?x0∈R,x3-x2-1>0” | |
| C. | 若p,q均为假命题,则p∧q为假命题 | |
| D. | 若a>b,则a2>b2. |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com