
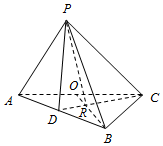
 在三棱锥P-ABC中,AB⊥BC,AB=6,$BC=2\sqrt{3}$,O为AC的中点,过C作BO的垂线,交BO、AB分别于R、D.若∠DPR=∠CPR,则三棱锥P-ABC体积的最大值为3$\sqrt{3}$.
在三棱锥P-ABC中,AB⊥BC,AB=6,$BC=2\sqrt{3}$,O为AC的中点,过C作BO的垂线,交BO、AB分别于R、D.若∠DPR=∠CPR,则三棱锥P-ABC体积的最大值为3$\sqrt{3}$. 分析 推导出AC=4$\sqrt{3}$,△BOC是正三角形,从而∠BCR=30°,CR=3,CD=4,进而DR=1,PR是∠DPC的平分线,$\frac{DP}{PC}=\frac{DR}{RC}=\frac{1}{3}$,由此能求出三棱锥P-ABC体积的最大值.
解答 解:∵AB⊥BC,AB=6,$BC=2\sqrt{3}$,∴AC=$\sqrt{36+12}$=4$\sqrt{3}$,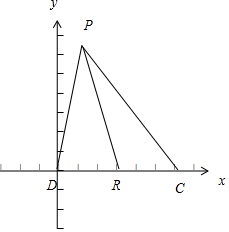
∴$∠BCA=\frac{BC}{AC}=\frac{1}{2}$,∴∠BCA=60°,
∵O为AC的中点,∴OA=OB=OC,∴△BOC是正三角形,
∵过C作BO的垂线,交BO、AB分别于R、D.∠DPR=∠CPR,
∴∠BCR=30°,CR=$\frac{\sqrt{3}}{2}BC=3$,CD=$\frac{2BC}{\sqrt{3}}$=4,∴DR=1,
∵∠DPR=∠CPR,∴PR是∠DPC的平分线,
∴$\frac{DP}{PC}=\frac{DR}{RC}=\frac{1}{3}$,
以D为原点,建立平面直角坐标系,如图,
设P(x,y),则$\frac{\sqrt{{x}^{2}+{y}^{2}}}{\sqrt{(x-4)^{2}+{y}^{2}}}$=$\frac{1}{3}$,
整理,得(x+$\frac{1}{2}$)+y2=$\frac{9}{4}$,
∴${y}_{max}=\frac{3}{2}$,
∴三棱锥P-ABC体积的最大值为:
Vmax=$\frac{1}{3}×{y}_{max}×{S}_{△ABC}$=$\frac{1}{3}×6×2\sqrt{3}×\frac{3}{2}$=3$\sqrt{3}$.
故答案为:3$\sqrt{3}$.
点评 本题考查三棱锥的体积的最大值的求法,考查推理论证能力、运算求解能力,考查等价转化思想、数形结合思想,考查空间思维能力,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{3}$ | B. | 2$\sqrt{5}$ | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{3}$ | B. | $\frac{16}{3}$ | C. | $\frac{4}{9}π$ | D. | $\frac{8}{3}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com