
分析 (1)由c=2$\sqrt{2}$,a=3,b2=a2-c2=1,即可求得椭圆C的标准方程;
(2)设直线l的方程,代入椭圆方程,由韦达定理及弦长公式即可求得线段AB的长度.
解答 解:(1)由为${F_1}({-2\sqrt{2},0}),{F_2}({2\sqrt{2},0})$,
焦点在x轴上,设椭圆方程:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0),c=2$\sqrt{2}$,
长轴长为6,2a=6,a=3,b2=a2-c2=1,
∴椭圆C的标准方程$\frac{{x}^{2}}{9}+{y}^{2}=1$;
(2)设A(x1,y1),B(x2,y2),
由(1)可知椭圆方程为$\frac{{x}^{2}}{9}+{y}^{2}=1$①,∵AB的方程为y=x+2,②
$\left\{\begin{array}{l}{y=x+2}\\{\frac{{x}^{2}}{9}+{y}^{2}=1}\end{array}\right.$,化简并整理得10x2+36x+27=0,
∴x1+x2=-$\frac{18}{5}$,x1x2=$\frac{27}{10}$,
又丨AB丨=$\sqrt{1+{k}^{2}}$•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{1+{1}^{2}}$•$\sqrt{(-\frac{18}{5})^{2}-4×\frac{27}{10}}$=$\frac{6\sqrt{3}}{5}$,
线段AB的长度$\frac{6\sqrt{3}}{5}$.
点评 本题考查椭圆的标准方程,直线与椭圆的位置关系,考查韦达定理,弦长公式,考查计算能力,属于中档题.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:高中数学 来源: 题型:选择题
| A. | y=sin2x | B. | y=|cosx| | C. | y=-tanx | D. | $y=cos\frac{x}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
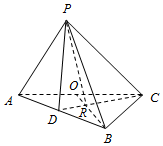 在三棱锥P-ABC中,AB⊥BC,AB=6,$BC=2\sqrt{3}$,O为AC的中点,过C作BO的垂线,交BO、AB分别于R、D.若∠DPR=∠CPR,则三棱锥P-ABC体积的最大值为3$\sqrt{3}$.
在三棱锥P-ABC中,AB⊥BC,AB=6,$BC=2\sqrt{3}$,O为AC的中点,过C作BO的垂线,交BO、AB分别于R、D.若∠DPR=∠CPR,则三棱锥P-ABC体积的最大值为3$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,3) | B. | (-1,2) | C. | (1,3) | D. | (2,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com