
| 喜爱运动 | 不喜爱运动 | 总计 | |
| 男 | 16 | ||
| 女 | 14 | ||
| 总计 | 30 |
| P(K2≥k0) | 0.40 | 0.25 | 0.10 | 0.010 |
| k0 | 0.708 | 1.323 | 2.706 | 6.635 |
| 喜爱运动 | 不喜爱运动 | 总计 | |
| 男 | 12 | 4 | 16 |
| 女 | 6 | 8 | 14 |
| 总计 | 18 | 12 | 30 |
| 30×(12×8-6×4)2 |
| (12+4)(6+8)(12+6)(4+8) |
| 3 |
| 5 |
| C | 0 3 |
| 3 |
| 5 |
| 2 |
| 5 |
| 8 |
| 125 |
| C | 1 3 |
| 3 |
| 5 |
| 2 |
| 5 |
| 36 |
| 125 |
| C | 2 3 |
| 2 |
| 5 |
| 3 |
| 5 |
| 54 |
| 125 |
| C | 3 3 |
| 3 |
| 5 |
| 27 |
| 125 |
| ξ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 3 |
| 5 |
| 3 |
| 5 |
| 9 |
| 5 |


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:
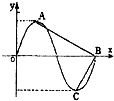 已知函数f(x)=
已知函数f(x)=| 3 |
| A、周期为4的奇函数 |
| B、周期为4的偶函数 |
| C、周期为2π的非奇非偶函数 |
| D、周期为4的非奇非偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:
A、
| ||
B、
| ||
| C、4 | ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图是一块不规则的铁皮,已知AB⊥BC,OA∥BC,AB=PC=2OA=4,曲线段OC是以点O为顶点,且开口向右的抛物线的一段,现用这块铁皮截出一块矩形铁皮,其中矩形的一对邻边分别在AB、BC上,且一个顶点P落在曲线段OC上,设点P到直线AB的距离为t+2,所截矩形铁皮的面积为S,则函数S=f(t)的图象大致是( )
如图是一块不规则的铁皮,已知AB⊥BC,OA∥BC,AB=PC=2OA=4,曲线段OC是以点O为顶点,且开口向右的抛物线的一段,现用这块铁皮截出一块矩形铁皮,其中矩形的一对邻边分别在AB、BC上,且一个顶点P落在曲线段OC上,设点P到直线AB的距离为t+2,所截矩形铁皮的面积为S,则函数S=f(t)的图象大致是( )A、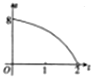 |
B、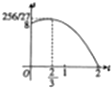 |
C、 |
D、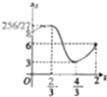 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x |
| 3 |
| 1 |
| 2 |
| 1 |
| 2014 |
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 2π |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| 2 |
| π |
| 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com