
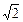 ,EF=EC=1,
,EF=EC=1, 
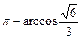
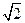 ,∴AC=BD=2;
,∴AC=BD=2; 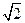 ,
,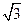 ,由勾股定理知 DF⊥EF,BF⊥EF,
,由勾股定理知 DF⊥EF,BF⊥EF, 由BF=DF=
由BF=DF=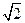 ,BD=2可知∠BFD=
,BD=2可知∠BFD=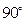 ,
,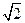 ,∴AM⊥BF,
,∴AM⊥BF,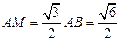 ,
,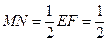 ;
;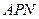 中,可求得
中,可求得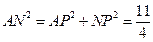 ,
, ∴在△
∴在△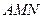 中,由余弦定理求得
中,由余弦定理求得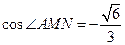 ,
,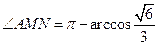 ……………………………(12分)
……………………………(12分)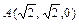

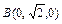 ,
,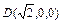 ,
,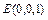 ,
,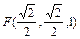 ,
,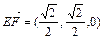 ,
,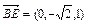 ,
,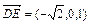 …(2分)
…(2分)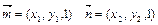 ,则
,则 ①
①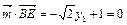 ②,
②,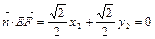 ③,
③, 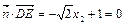 ④.
④.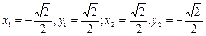 ,∴
,∴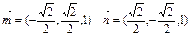 ,…(4分)
,…(4分)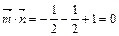 ,∴
,∴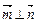 ,故平面BEF⊥平面DEF…………(6分)
,故平面BEF⊥平面DEF…………(6分)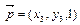 ,∵
,∵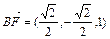 ,
,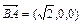
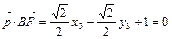 ,
,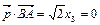 ,解得
,解得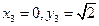
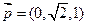 ,………(8分)∴
,………(8分)∴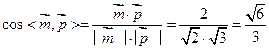 ……(10分)
……(10分)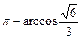


科目:高中数学 来源:不详 题型:解答题
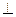 平面ABEF,如图所示,FD
平面ABEF,如图所示,FD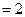 , AD=1, EF=
, AD=1, EF=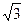 .
.
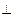 平面FCB;
平面FCB;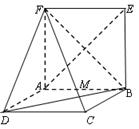
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
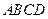 所在平面与平面四边形
所在平面与平面四边形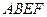 所在平面互相垂直,△
所在平面互相垂直,△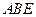 是等腰直角三角形,
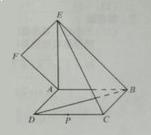
是等腰直角三角形,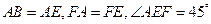 。
。
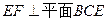 ;
;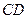 的中点为
的中点为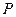 ,在直线
,在直线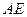 上是否存在一点
上是否存在一点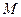 ,使得
,使得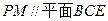 ?若存在,请指出点
?若存在,请指出点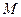 的位置,并证明你的结论;若不存在,请说明理由;
的位置,并证明你的结论;若不存在,请说明理由;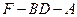 的大小。
的大小。查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
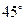 纬线上有A,B两点,设该纬线圈上A,B两点的劣弧长为
纬线上有A,B两点,设该纬线圈上A,B两点的劣弧长为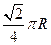 ,(R为地球半径),则A,B两点间的球面距离为__________________.
,(R为地球半径),则A,B两点间的球面距离为__________________.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
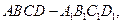
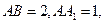
 直线
直线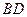 与平面
与平面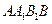 所成的角为
所成的角为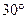 ,
,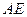 垂直
垂直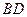 于
于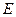 ,
,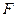 为
为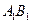 的中点.
的中点.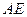 与
与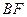 所成的角;
所成的角;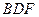 与平面
与平面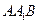 所成的二面角;
所成的二面角;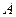 到平面
到平面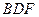 的距离.
的距离.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com