
| A. | [3,+∞) | B. | (-∞,3] | C. | (-∞,6] | D. | [6,+∞) |
分析 利用基本不等式求得a+b的最小值,把问题转化为m≥-x2+4x+2对任意实数x恒成立,再利用配方法求出-x2+4x+2的最大值得答案.
解答 解:∵a>0,b>0,且$\frac{1}{a}$+$\frac{9}{b}$=1,
∴a+b=(a+b)($\frac{1}{a}+\frac{9}{b}$)=10+$\frac{b}{a}+\frac{9a}{b}$$≥10+2\sqrt{\frac{b}{a}•\frac{9a}{b}}=16$.
当且仅当3a=b,即a=4,b=12时,(a+b)min=16.
若不等式a+b≥-x2+4x+18-m对任意实数x恒成立,
则-x2+4x+18-m≤16,即m≥-x2+4x+2对任意实数x恒成立,
∵-x2+4x+2=-(x-2)2+6≤6,
∴m≥6.
∴实数m的取值范围是[6,+∞).
故选:D.
点评 本题考查恒成立问题,考查利用基本不等式求最值,训练了分离变量法求字母的取值问题,是中档题.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:解答题
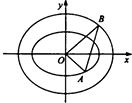 如图,在平面直角坐标系xOy中,A和B分别是椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)和C2:$\frac{{x}^{2}}{{m}^{2}}$+$\frac{{y}^{2}}{{n}^{2}}$=1(m>n>0)上的动点,已知C1的焦距为2,且$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,又当动点A在x轴上的射影为C1的焦点时,点A恰在双曲线2y2-x2=1的渐近线上.
如图,在平面直角坐标系xOy中,A和B分别是椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)和C2:$\frac{{x}^{2}}{{m}^{2}}$+$\frac{{y}^{2}}{{n}^{2}}$=1(m>n>0)上的动点,已知C1的焦距为2,且$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,又当动点A在x轴上的射影为C1的焦点时,点A恰在双曲线2y2-x2=1的渐近线上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=$\frac{1}{x}$ | B. | y=e-x | C. | y=1-x2 | D. | y=lg|x| |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{81}$ | B. | $\frac{4}{27}$ | C. | $\frac{4}{9}$ | D. | $\frac{8}{27}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com