
���� ��1��ҪʹԲO��x2+y2=r2������һ������l����Բ$M��\frac{x^2}{6}+\frac{y^2}{3}=1$����������ͬ�Ľ��㣬��Բ������Բ���ڲ����ɣ�
��2��������ߵķ��̣�������Բ���̣�����Τ�ﶨ������ֱ�ߴ�ֱ���������������������ɵõ��뾶r��ֵ����OA��OB����$|{\overrightarrow{OA}}|•|{\overrightarrow{OB}}|$=r•AB���ɵ�$|{\overrightarrow{OA}}|•|{\overrightarrow{OB}}|$�����ֵ��
��� �⣺��1��ҪʹԲO��x2+y2=r2������һ������l����Բ$M��\frac{x^2}{6}+\frac{y^2}{3}=1$����������ͬ�Ľ��㣬
��Բ������Բ���ڲ�����0��r��$\sqrt{3}$��
��2����Բ�����߷���y=kx+m����$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{x}^{2}}{6}+\frac{{y}^{2}}{3}=1}\end{array}\right.$���ã�1+2k2��x2+4kmx+2m2-6=0��
��A��x1��y1����B��x2��y2����x1+x2=$\frac{-4km}{1+2{k}^{2}}$��x1x2=$\frac{2{m}^{2}-6}{1+2{k}^{2}}$��
y1y2=��kx1+m����kx2+m��=$\frac{{m}^{2}-6{k}^{2}}{1+2{k}^{2}}$��
��OA��OB����x1x2+y1y2=0⇒m2=2k2+2������
��y=kx+m��ԲO��x2+y2=r2���У���r2=$\frac{{m}^{2}}{1+{k}^{2}}$����
�ɢ٢ڵ�r2=2����ʱԲ�ķ���Ϊ��x2+y2=2��
�����ߵ�б�ʲ�����ʱ�����߷���Ϊx=��$\sqrt{2}$
A��$\sqrt{2}��\sqrt{2}$����B��$\sqrt{2}��-\sqrt{2}$����A��-$\sqrt{2��}\sqrt{2}$����B��-$\sqrt{2��}-\sqrt{2}$����������
��Բ�ķ���Ϊ��x2+y2=2
��|AB|=$\sqrt{1+{k}^{2}}\sqrt{��{x}_{1}+{x}_{2}��^{2}-4{x}_{1}{x}_{2}}$=$2\sqrt{2}\sqrt{1+\frac{1}{4{k}^{2}+\frac{1}{{k}^{2}}+4}}��3$��
��ֱ��AB��б�ʲ����ڻ�Ϊ0ʱ��|AB|=2$\sqrt{2}$��
��|AB|��3
��OA��OB����$|{\overrightarrow{OA}}|•|{\overrightarrow{OB}}|$=r•AB��
$|{\overrightarrow{OA}}|•|{\overrightarrow{OB}}|$�����ֵ3$\sqrt{2}$��
���� ����ֱ�ߺ�Բ���У��Լ�ֱ�ߺ���Բ��������Τ�ﶨ������ֱ�ߴ�ֱ��������������Ϊ0�����黯���ں��������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
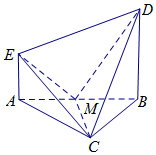 ��ͼ��EA��ƽ��ABC��DB��ƽ��ABC����ABC�ǵȱ������Σ�AC=2AE��M��AB���е㣮
��ͼ��EA��ƽ��ABC��DB��ƽ��ABC����ABC�ǵȱ������Σ�AC=2AE��M��AB���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1 | B�� | -2 | C�� | -3 | D�� | 1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3�� | B�� | $\frac{3��}{2}$ | C�� | 6�� | D�� | $\frac{3��}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | $\frac{{\sqrt{3}}}{2}$ | C�� | $\sqrt{2}$ | D�� | $\frac{{\sqrt{6}}}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1 | B�� | 0 | C�� | 1 | D�� | e |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��0��1] | B�� | ��0��2�� | C�� | $��{0��\frac{3}{2}}]$ | D�� | ��0��2] |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com