练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    17．如果函数y=b与函数y=x2-3|x-1|-4x-3的图象恰好有三个交点，则b=$-6或-\frac{25}{4}$．

    分析 按x≥1和x＜1分别去绝对值，得到分段函数，确定两函数图象的交点坐标，顶点坐标，结合分段函数的自变量取值范围求出符合条件的b的值．

    解答 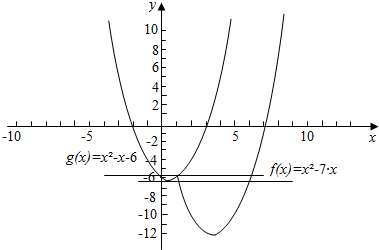解：当x≥1时，函数y=x2-7x
    图象的一个端点为（1，-6），顶点坐标为$（\frac{7}{2}，-\frac{49}{4}）$，
    当x＜1时，函数y=x2-x-6．
    顶点坐标为$（\frac{1}{2}，-\frac{25}{4}）$，
    ∴当b=-6或$b=-\frac{25}{4}$时，两图象恰有三个交点．
    故答案为：$-6或-\frac{25}{4}$．

    点评 本题考查了分段的两个二次函数的性质，根据绝对值里式子的符号分类，得到两个二次函数是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    2．函数f（x）=2sinx+cosx的最小值为-$\sqrt{5}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．已知复数z=1-2i，则适合不等式|z+ai|≤$\sqrt{2}$的实数a的取值范围是[1，3]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．已知几何体的三视图如图，则这个几何体自上而下依次是（　　）
    A．四棱台，圆台B．四棱台，四棱台C．四棱柱，四棱柱D．不能判断

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．在等比数列{an}中，公比q＞1，a2=2，前三项和S3=7．
    （Ⅰ）求数列{an}的通项公式；
    （Ⅱ）记bn=log2an，cn=$\frac{1}{{b}_{n+1}•{b}_{n+2}}$，求数列{an}的前n项和Tn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．已知函数f（x）=ex-mx+1的图象是曲线C，若曲线C不存在与直线y=ex垂直的切线，则实数m的取值范围是（　　）
    A．（-∞，-$\frac{1}{e}$）B．[$\frac{1}{e}$，+∞）C．（-∞，$\frac{1}{e}$）D．（-∞，$\frac{1}{e}$]

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．抛物线y2=x上的点到直线x-2y+3=0的距离最短的点的坐标是（1，-1）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．设全集U={a，b，c，d，e}，集合A={a，b，c，d}，B={c，d，e}，则集合∁U（A∩B）=（　　）
    A．{d}B．{a，b}C．{b，c，d}D．{a，b，e}

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．已知全集U=R，$A=\left\{{x|{x^2}-3x=0}\right\}，B=\left\{{x|x＞\frac{1}{4}}\right\}$，则A∩∁UB={0}．

    查看答案和解析>>

    同步练习册答案