
【题目】一只红铃虫的产卵数![]() 和温度
和温度![]() 有关,现收集了6组观测数据如下表:
有关,现收集了6组观测数据如下表:
温度 | 21 | 24 | 25 | 27 | 29 | 32 |
产卵数 | 7 | 11 | 21 | 24 | 66 | 115 |
| 1.946 | 2.398 | 3.045 | 3.178 | 4.191 | 4.745 |
(I)以温度为23、25、27、29的数据分别建立:①![]() 和
和![]() 之间线性回归方程
之间线性回归方程![]() ,②
,②![]() 和
和![]() 之间线性回归方程
之间线性回归方程![]() ;
;
(Ⅱ)若以(Ⅰ)所得回归方程预测,得到温度为21、32的数据如下:
温度 | 21 | 32 |
| -11.5 | 80.94 |
| 1.825 | 4.857 |
试以上表数据说明①②两个模型,哪个拟合的效果更好.
参考数据:![]()
![]()
![]()
科目:高中数学 来源: 题型:
【题目】目前某地区有100万人,经过x年后为y万人,如果年平均增长率是1.2%,请回答下列问题:
(1)试推算出y关于x的函数关系式;
(2)计算10年后该地区的人口总数(精确到0.1万人);
(3)计算大约多少年后该地区的人口总数会达到120万(精确到1年).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知袋中装有大小相同的2个白球、2个红球和1个黄球.一项游戏规定:每个白球、红球和黄球的分值分别是0分、1分和2分,每一局从袋中一次性取出三个球,将3个球对应的分值相加后称为该局的得分,计算完得分后将球放回袋中.当出现第![]() 局得
局得![]() 分(
分(![]() )的情况就算游戏过关,同时游戏结束,若四局过后仍未过关,游戏也结束.
)的情况就算游戏过关,同时游戏结束,若四局过后仍未过关,游戏也结束.
(1)求在一局游戏中得3分的概率;
(2)求游戏结束时局数![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面是追踪调查200个某种电子元件寿命(单位:![]() )频率分布直方图,如图:
)频率分布直方图,如图:
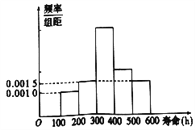
其中300-400、400-500两组数据丢失,下面四个说法中有且只有一个与原数据相符,这个说法是( )
①寿命在300-400的频数是90;
②寿命在400-500的矩形的面积是0.2;
③用频率分布直方图估计电子元件的平均寿命为:
![]()
④寿命超过![]() 的频率为0.3
的频率为0.3
A. ① B. ② C. ③ D. ④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解高校学生平均每天使用手机的时间长短是否与性别有关,某调查小组随机抽取了25 名男生、10名女生进行为期一周的跟踪调查,调查结果如表所示:
平均每天使用手机 | 平均每天使用手机 | 合计 | |
男生 | 15 | 10 | 25 |
女生 | 3 | 7 | 10 |
合计 | 18 | 17 | 35 |
(I) 根据列联表判断,是否有90%的把握认为学生使用手机的时间长短与性别有关;
(II)在参与调查的平均每天使用手机不超过3小时的10名男生中,有6人使用国产手机,从这10名男生中任意选取3人,求这3人中使用国产手机的人数![]() 的分布列和数学期望.
的分布列和数学期望.
| 0.400 | 0.250 | 0.150 | 0.100 | 0.050 | 0.025 |
| 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
参考公式:![]()
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列随机事件:
①某射手射击一次,可能命中![]() 环,
环,![]() 环,
环,![]() 环,
环,![]() ,
,![]() 环;
环;
②一个小组有男生![]() 人,女生
人,女生![]() 人,从中任选
人,从中任选![]() 人进行活动汇报;
人进行活动汇报;
③一只使用中的灯泡寿命长短;
④抛出一枚质地均匀的硬币,观察其出现正面或反面的情况;
⑤中秋节前夕,某市有关部门调查辖区内某品牌的月饼质量,给该品牌月饼评“优”或“差”.
这些事件中,属于古典概型的是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若方程![]() 所表示的曲线为C,给出下列四个命题:
所表示的曲线为C,给出下列四个命题:
①若C为椭圆,则![]() ;
;
②若C为双曲线,则![]() 或
或![]() ;
;
③曲线C不可能是圆;
④若![]() ,曲线C为椭圆,且焦点坐标为
,曲线C为椭圆,且焦点坐标为![]() ;
;
⑤若![]() ,曲线C为双曲线,且虚半轴长为
,曲线C为双曲线,且虚半轴长为![]() .
.
其中真命题的序号为____________.(把所有正确命题的序号都填在横线上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C:x2-y2=1及直线l:y=kx-1.
(1)若l与C有两个不同的交点,求实数k的取值范围;
(2)若l与C交于A,B两点,O为坐标原点,且△AOB的面积为![]() ,求实数k的值.
,求实数k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com