
| A. | f(2a)<f(2)<f(log2a) | B. | $f(2)<f({log_2}a)<f({2^a})$ | C. | $f({log_2}a)<f({2^a})<f(2)$ | D. | $f({log_2}a)<f(2)<f({2^a})$ |
分析 函数f(x)对任意的x∈R都有f(x)=f(2-x),则函数f(x)关于直线x=1对称.当x≠1时,其导函数f'(x)满足xf'(x)>f'(x),可得(x-1)f′(x)>0,进而得到单调性.若1<a<2,则0<log2a<1<2<2a,f(log2a)=f(2-log2a),2-log2a∈(1,2),即可得出.
解答 解:函数f(x)对任意的x∈R都有f(x)=f(2-x),则函数f(x)关于直线x=1对称.
当x≠1时,其导函数f'(x)满足xf'(x)>f'(x),则(x-1)f′(x)>0,
x>1时,f′(x)>0,此时函数f(x)单调递增;x<1时,f′(x)<0,此时函数f(x)单调递减.
若1<a<2,则0<log2a<1<2<2a,f(log2a)=f(2-log2a),2-log2a∈(1,2),
∴f(log2a)=f(2-log2a)<f(2)<f(2a),
故选:D.
点评 本题考查了利用导数研究函数的单调性、分类讨论方法、转化方法,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | y=$\sqrt{{x}^{2}}$ | B. | y=$\frac{{x}^{2}}{x}$ | ||
| C. | y=($\sqrt{x}$)2 | D. | y=logaax(a>0且a≠1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
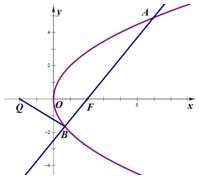 已知抛物线E:y2=2px(p>0)的准线是圆C:(x-1)2+y2=4的切线.
已知抛物线E:y2=2px(p>0)的准线是圆C:(x-1)2+y2=4的切线.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 数学成绩好 | 数学成绩一般 | 总计 | |
| 物理成绩好 | |||
| 物理成绩一般 | |||
| 总计 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p是假命题,¬p:?x∈(0,$\frac{π}{2}$),f(x)≥0 | B. | p是假命题,¬p:?x∈(0,$\frac{π}{2}$),f(x)≥0 | ||
| C. | p是真命题,¬p:?x∈(0,$\frac{π}{2}$),f(x)≥0 | D. | p是真命题,¬p:?x∈(0,$\frac{π}{2}$),f(x)≥0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com