练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知命题p：“?a＞0，有ea≥1成立”，则￢p为（　　）
    A、?a≤0，有ea≤1成立B、?a≤0，有ea≥1成立C、?a＞0，有ea＜1成立D、?a＞0，有ea≤1成立
    考点：命题的否定
    专题：简易逻辑
    分析：根据全称命题的否定是特称命题即可得到结论．
    解答：解：全称命题的否定是特称命题，则￢p：?a＞0，有ea＜1成立，
    故选：C．
    点评：本题主要考查含有量词的命题的否定，比较基础．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知
    a
    =（
    		3
    （cosωx+sinωx），sinωx），
    b
    =（cosωx-sinωx，2cosωx）．函数f（x）=
    a
    •
    b
    ，其中ω＞0，且f（x）的最小正周期为π．
    （Ⅰ） 求f（x）的单调递增区间；
    （Ⅱ） 利用五点法作出f（x）在[
    π
    6
    ，
    5π
    6
    ]上的图象．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    《张邱建算经》有一道题：今有女子不善织布，逐日所织的布同数递减，初日织五尺，末一日织一尺，计织三十日，问共织布（　　）
    A、110尺B、90尺C、60尺D、30尺

    查看答案和解析>>

    科目：高中数学 来源： 题型：

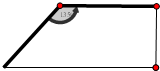    两直立矮墙成135°二面角，现利用这两面矮墙和篱笆围成一个面积为54m2的直角梯形菜园（墙足够长），则所用篱笆总长度的最小值为（　　）
    A、16m
    B、18m
    C、22.5m
    D、15
    		3
    m

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知命题p：a=1是?x＞0，x+
    a
    x
    ≥2的充要条件：命题q：?x∈R，x2-x+1＜0．则下列结论中正确的是（　　）
    A、p∧q为真命题
    B、p∧￢q为真命题
    C、￢p∧q为真命题
    D、￢p∧￢q为真命题

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下列命题：
    ①G2=ab是三个数a、G、b成等比数列的充要条件；
    ②若y=f（x）不恒为0，且对于?x∈R，都有f（x+2）=-f（x），则f（x）是周期函数；
    ③对于命题p：?x∈R，2x+3＞0，则￢p：?x0∈R，2x0+3＜0；
    ④直线l：
    		2
    x+
    		2
    y+1+a=0与圆C：x2+y2=a（a＞0）相离．
    其中不正确命题的个数为（　　）
    A、1B、2C、3D、4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    定义“正对数”：ln+x=
    0，0＜x＜1
    lnx，x≥1
    ，现有四个命题：
    ①若a＞0，b＞0，则ln+（ab）=bln+a
    ②若a＞0，b＞0，则ln+（ab）=ln+a+ln+b
    ③若a＞0，b＞0，则ln+(
    a
    b
    )≥ln+a-ln+b
    ④若a＞0，b＞0，则ln+（a+b）≤ln+a+ln+b+ln2
    其中正确的命题有（　　）
    A、①③④B、①②③
    C、①②④D、②③④

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若p：φ=
    π
    2
    +kπ，k∈Z，q：f（x）=sin（ωx+φ）（ω≠0）是偶函数，则p是q的（　　）
    A、充要条件
    B、充分不必要条件
    C、必要不充分条件
    D、既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知两点A（1，-2），B（-4，-2），以下列四条曲线：
    ①4x+2y=3；
    ②x2+y2=3；
    ③x2+2y2=3；
    ④x2-2y2=3．
    其中存在点P，使|PA|=|PB|的曲线有（　　）
    A、①③B、②④C、①②③D、②③④

    查看答案和解析>>

    同步练习册答案