
分析 由圆的方程为求得圆心C,半径r,由“若四边形面积最小,则圆心与点P的距离最小时,即距离为圆心到直线的距离时,切线长PA,PB最小”,最后利用点到直线的距离求出直线的斜率即可..
解答 解:∵圆的方程为:x2+(y+1)2=1,
∴圆心C(0,-1),半径r=1.
根据题意,若四边形面积最小,当圆心与点P的距离最小时,即距离为圆心到直线l的距离最小时,切线长PA,PB最小.切线长为$\sqrt{2}$,
∴PA=PB═$\sqrt{2}$,
∴圆心到直线l的距离为d=$\sqrt{3}$.
∵直线kx+y-2=0,
∴$\sqrt{3}$=$\frac{3}{\sqrt{{k}^{2}+1}}$,解得k=±$\sqrt{2}$,
所求直线的斜率为$±\sqrt{2}$
故答案为:$±\sqrt{2}$.
点评 本题的考点是直线与圆的位置关系,主要涉及了构造四边形及其面积的求法,解题的关键是“若四边形面积最小,则圆心与点P的距离最小时,即距离为圆心到直线的距离时,切线长PA,PB最小”属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
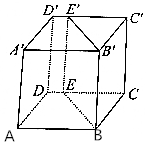 如图,过正方体ABCD-A′B′C′D′的棱BB′作一平面交平面CDD′C′于EE′,则BB′与EE′的位置关系是( )
如图,过正方体ABCD-A′B′C′D′的棱BB′作一平面交平面CDD′C′于EE′,则BB′与EE′的位置关系是( )| A. | 平行 | B. | 相交 | C. | 异面 | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
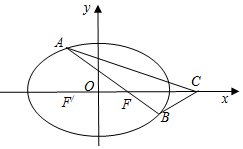 已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)经过点P(1,$\frac{3}{2}$),离心率e=$\frac{1}{2}$.
已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)经过点P(1,$\frac{3}{2}$),离心率e=$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
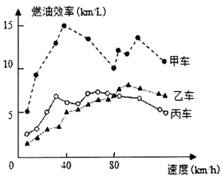 汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,如图描述了甲、乙、丙三辆汽车在不同速度下燃油效率情况,下列叙述中正确的是( )
汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,如图描述了甲、乙、丙三辆汽车在不同速度下燃油效率情况,下列叙述中正确的是( )| A. | 消耗1升汽油,乙车最多可行驶5千米 | |
| B. | 以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多 | |
| C. | 某城市机动车最高限速80千米/小时,相同条件下,在该市用丙车比用乙车更省油 | |
| D. | 甲车以80千米/小时的速度行驶1小时,消耗10升汽油 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com