
| A. | $\sqrt{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
分析 写出直线的点斜式方程,与抛物线方程联立得出A,B两点的坐标关系,根据kAM•kBM=-1列方程解出k.
解答 解:抛物线焦点F(2,0),设直线AB的方程为y=k(x-2),
联立方程组$\left\{\begin{array}{l}{{y}^{2}=8x}\\{y=k(x-2)}\end{array}\right.$,消元得k2x-(4k2+8)x+4k2=0.
设A(x1,y1),B(x2,y2),则x1+x2=4+$\frac{8}{{k}^{2}}$,x1x2=4.
∴y1+y2=k(x1+x2)-4k=$\frac{8}{k}$,y1y2=-16.
∵∠AMB=90°,∴kAM•kBM=-1,即$\frac{{y}_{1}-2}{{x}_{1}+2}•\frac{{y}_{2}-2}{{x}_{2}+2}=-1$.
∴y1y2-2(y1+y2)+4+x1x2+2(x1+x2)+4=0.
∴-16-$\frac{16}{k}$+4+4+2(4+$\frac{8}{{k}^{2}}$)+4=0,整理得:k2-4k+4=0,
解得k=2.
故选:D.
点评 本题考查了抛物线的性质,直线与抛物线的位置关系,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$或$\frac{3π}{4}$ | B. | $\frac{π}{3}$或$\frac{2π}{3}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
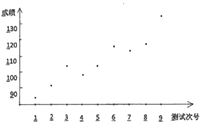 对某高三学生在连续9次数学测试中的成绩(单位:分)进行统计得到如图散点图.下面关于这位同学的数学成绩的分析中,正确的共有( )个
对某高三学生在连续9次数学测试中的成绩(单位:分)进行统计得到如图散点图.下面关于这位同学的数学成绩的分析中,正确的共有( )个| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com