
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程是
的参数方程是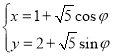 (
(![]() 是参数).以坐标原点
是参数).以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,其倾斜角为
,其倾斜角为![]() .
.
(Ⅰ)证明直线![]() 恒过定点
恒过定点![]() ,并写出直线
,并写出直线![]() 的参数方程;
的参数方程;
(Ⅱ)在(Ⅰ)的条件下,若直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】下列四个命题,其中正确的是( )
A.对分类变量![]() 与
与![]() 的随机变量
的随机变量![]() 的观测值
的观测值![]() 来说,
来说,![]() 越小,“
越小,“![]() 与
与![]() 有关系”可信程度越大
有关系”可信程度越大
B.残差点比较均匀地落在水平带状区域内,带状区域越窄,则模型拟合精度越高
C.相关指数![]() 越小,则残差平方和越大,模型的拟合效果越好
越小,则残差平方和越大,模型的拟合效果越好
D.两个随机变量相关性越强,则相关系数的绝对值越接近![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了响应党的十九大所提出的教育教学改革,某校启动了数学教学方法的探索,学校将高一年级部分生源情况基本相同的学生分成甲、乙两个班,每班40人,甲班按原有传统模式教学,乙班实施自主学习模式.经过一年的教学实验,将甲、乙两个班学生一年来的数学成绩取平均数,两个班学生的平均成绩均在![]() ,按照区间
,按照区间![]() ,
,![]() ,
,![]() ,
,![]() ,
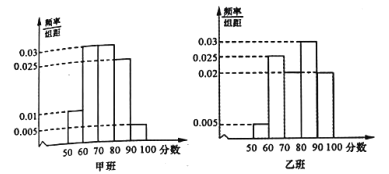
,![]() 进行分组,绘制成如下频率分布直方图,规定不低于80分(百分制)为优秀.
进行分组,绘制成如下频率分布直方图,规定不低于80分(百分制)为优秀.
| 0.10 | 0.05 | 0.025 |
| 2.706 | 3.841 | 5.024 |
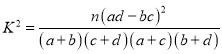
(1)完成表格,并判断是否有![]() 以上的把握认为“数学成绩优秀与教学改革有关”;
以上的把握认为“数学成绩优秀与教学改革有关”;
甲班 | 乙班 | 合计 | |
大于等于80分的人数 | |||
小于80分的人数 | |||
合计 |
(2)从乙班![]() ,
,![]() ,
,![]() 分数段中,按分层抽样随机抽取7名学生座谈,从中选三位同学发言,记来自
分数段中,按分层抽样随机抽取7名学生座谈,从中选三位同学发言,记来自![]() 发言的人数为随机变量
发言的人数为随机变量![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】每年10月中上旬是小麦的最佳种植时间,但小麦的发芽会受到土壤、气候等多方面因素的影响.某科技小组为了解昼夜温差的大小与小麦发芽的多少之间的关系,在不同的温差下统计了100颗小麦种子的发芽数,得到了如下数据:
温差 | 8 | 10 | 11 | 12 | 13 |
发芽数 | 79 | 81 | 85 | 86 | 90 |
(1)请根据统计的最后三组数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若由(1)中的线性回归方程得到的估计值与前两组数据的实际值误差均不超过两颗,则认为线性回归方程是可靠的,试判断(1)中得到的线性回归方程是否可靠;
(3)若100颗小麦种子的发芽率为![]() 颗,则记为
颗,则记为![]() 的发芽率,当发芽率为
的发芽率,当发芽率为![]() 时,平均每亩地的收益为
时,平均每亩地的收益为![]() 元,某农场有土地10万亩,小麦种植期间昼夜温差大约为
元,某农场有土地10万亩,小麦种植期间昼夜温差大约为![]() ,根据(1)中得到的线性回归方程估计该农场种植小麦所获得的收益.
,根据(1)中得到的线性回归方程估计该农场种植小麦所获得的收益.
附:在线性回归方程![]() 中,
中,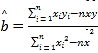 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
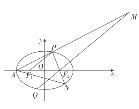
【题目】已知椭圆![]() 的左顶点为
的左顶点为![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,离心率为
,离心率为![]() ,
,![]() 是椭圆上的一个动点(不与左、右顶点重合),且
是椭圆上的一个动点(不与左、右顶点重合),且![]() 的周长为6,点
的周长为6,点![]() 关于原点的对称点为
关于原点的对称点为![]() ,直线
,直线![]() 交于点
交于点![]() .
.
(1)求椭圆方程;
(2)若直线![]() 与椭圆交于另一点
与椭圆交于另一点![]() ,且
,且![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com