
【题目】下列四个命题,其中正确的是( )
A.对分类变量![]() 与
与![]() 的随机变量
的随机变量![]() 的观测值
的观测值![]() 来说,
来说,![]() 越小,“
越小,“![]() 与
与![]() 有关系”可信程度越大
有关系”可信程度越大
B.残差点比较均匀地落在水平带状区域内,带状区域越窄,则模型拟合精度越高
C.相关指数![]() 越小,则残差平方和越大,模型的拟合效果越好
越小,则残差平方和越大,模型的拟合效果越好
D.两个随机变量相关性越强,则相关系数的绝对值越接近![]()
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案科目:高中数学 来源: 题型:
【题目】选修![]() :不等式选讲
:不等式选讲
已知函数f(x)=|2x+3|+|2x﹣1|.
(Ⅰ)求不等式f(x)<8的解集;
(Ⅱ)若关于x的不等式f(x)≤|3m+1|有解,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的内接等边三角形
的内接等边三角形![]() 的面积为
的面积为![]() (其中
(其中![]() 为坐标原点).
为坐标原点).
(1)试求抛物线![]() 的方程;
的方程;
(2)已知点![]() 两点在抛物线
两点在抛物线![]() 上,
上,![]() 是以点
是以点![]() 为直角顶点的直角三角形.
为直角顶点的直角三角形.
①求证:直线![]() 恒过定点;
恒过定点;
②过点![]() 作直线
作直线![]() 的垂线交
的垂线交![]() 于点
于点![]() ,试求点
,试求点![]() 的轨迹方程,并说明其轨迹是何种曲线.
的轨迹方程,并说明其轨迹是何种曲线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系![]() 中,直线l的参数方程为
中,直线l的参数方程为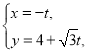 (
(![]() 为参数),曲线
为参数),曲线![]() 的方程为
的方程为![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求直线l和曲线![]() 的极坐标方程;
的极坐标方程;
(2)曲线![]() 分别交直线和曲线
分别交直线和曲线![]() 于点
于点![]() ,求
,求![]() 的最大值及相应的
的最大值及相应的![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一某班的某次数学测试成绩(满分为100分)的茎叶图和频率分布直方图都受了不同程度的破坏,但可见部分如图,据此解答下列问题:
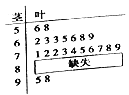
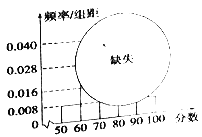
(1)求分数在![]() 的频率及全班人数;
的频率及全班人数;
(2)求分数在![]() 之间的频数,并计算频率分布直方图中
之间的频数,并计算频率分布直方图中![]() 间的矩形的高.
间的矩形的高.
(3)若从分数在![]() 和分数在90分以上的试卷选3份试卷进行试卷分析,求最高分的试卷被抽中的概率.
和分数在90分以上的试卷选3份试卷进行试卷分析,求最高分的试卷被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() (
(![]() ),圆
),圆![]() (
(![]() ),若圆
),若圆![]() 的一条切线
的一条切线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点.
两点.
(1)当![]() ,
, ![]() 时,若点
时,若点![]() 都在坐标轴的正半轴上,求椭圆
都在坐标轴的正半轴上,求椭圆![]() 的方程;
的方程;
(2)若以![]() 为直径的圆经过坐标原点
为直径的圆经过坐标原点![]() ,探究
,探究![]() 是否满足
是否满足![]() ,并说明理由.
,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为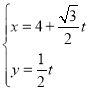 (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]()
(1)在曲线![]() 上任取一点
上任取一点![]() ,连接
,连接![]() ,在射线
,在射线![]() 上取一点
上取一点![]() ,使
,使![]() ,求
,求![]() 点轨迹的极坐标方程;
点轨迹的极坐标方程;
(2)在曲线![]() 上任取一点
上任取一点![]() ,在曲线
,在曲线![]() 上任取一点
上任取一点![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程是
的参数方程是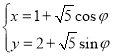 (
(![]() 是参数).以坐标原点
是参数).以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,其倾斜角为
,其倾斜角为![]() .
.
(Ⅰ)证明直线![]() 恒过定点
恒过定点![]() ,并写出直线
,并写出直线![]() 的参数方程;
的参数方程;
(Ⅱ)在(Ⅰ)的条件下,若直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com