
分析 ①根据向量关系的等价条件进行判断,
②根据对数和指数幂的运算性质进行判断,
③根据直线垂直的等价条件进行判断,
④根据基本不等式的性质进行判断即可.
解答 解:①若$|{\overrightarrow a+\overrightarrow b}|=|{\overrightarrow a}|-|{\overrightarrow b}|$,则$\overrightarrow{a}$与$\overrightarrow{b}$共线,且方向相反,即存在实数λ,使得$\overrightarrow b=λ\overrightarrow a$成立;故①正确,
②log${\;}_{\frac{1}{3}}$2=-log32∈(-1,0),b=log${\;}_{\frac{1}{2}}$3=-log23<-1,($\frac{1}{3}$)0.5>0,则c>a>b,故②正确,
③当b=0,a=0时,两直线分别为l1:3y-1=0,l2:x+1=0,满足l1⊥l2,故l1⊥l2的充要条件是$\frac{a}{b}=-3$错误,故③错误,
④已知a>0,b>0,函数y=2aex+b的图象过点(0,1),则2a+b=1,则$\frac{1}{a}+\frac{1}{b}$=($\frac{1}{a}+\frac{1}{b}$)(2a+b)=2+1+$\frac{2a}{b}$+$\frac{b}{a}$≥3+2$\sqrt{\frac{2a}{b}•\frac{b}{a}}$=3+2$\sqrt{2}$,
即则$\frac{1}{a}+\frac{1}{b}$的最小值是3+2.故④错误,
故答案为:①②
点评 本题主要考查命题的真假判断,涉及的知识点较多,综合性较强,但难度不大.


科目:高中数学 来源: 题型:选择题
| A. | p是真命题且q是假命题 | B. | p是真命题且q是真命题 | ||
| C. | p是假命题且q是真命题 | D. | p是真命题且q是假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
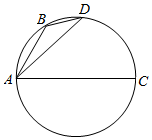 如图,B、D是以AC为直径的圆上的两点,其中$AB=\sqrt{t+1}$,$AD=\sqrt{t+2}$,则$\overrightarrow{AC}$$•\overrightarrow{BD}$=( )
如图,B、D是以AC为直径的圆上的两点,其中$AB=\sqrt{t+1}$,$AD=\sqrt{t+2}$,则$\overrightarrow{AC}$$•\overrightarrow{BD}$=( )| A. | 1 | B. | 2 | C. | t | D. | 2t |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com