
【题目】已知数列![]() 和
和![]() 的前
的前![]() 项和分别为
项和分别为![]() 和
和![]() ,且
,且![]() ,
,![]() ,
,![]() ,其中
,其中![]() 为常数.
为常数.
(1)若![]() ,
,![]() .
.
①求数列![]() 的通项公式;
的通项公式;
②求数列![]() 的通项公式.
的通项公式.
(2)若![]() ,
,![]() .求证:
.求证:![]() .
.
【答案】(1)①![]() ,②
,②![]() (2)见解析.
(2)见解析.
【解析】
(1)①已知两等式相加可得![]() 是等比数列,从而可得通项公式,②已知两等式相减可得
是等比数列,从而可得通项公式,②已知两等式相减可得![]() 的递推关系式,凑配成一个新的等比数列,利用等比数列的通项公式可求得
的递推关系式,凑配成一个新的等比数列,利用等比数列的通项公式可求得![]() ;
;
(2)已知两等式相加可得数列![]() 是等比数列,
是等比数列,![]() 就是
就是![]() 的前
的前![]() 项和,分类求得这个和,在
项和,分类求得这个和,在![]() 且
且![]() 时用数学归纳法证明不等式成立.
时用数学归纳法证明不等式成立.
(1)若![]() ,
,![]() ,则有
,则有
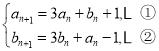
由![]() ,得:
,得:![]()
所以![]() 是公比为4的等比数列,首项
是公比为4的等比数列,首项![]() ,
,
所以![]() ;
;
由![]() ,得:
,得:![]()
则![]()
所以![]() 是公比为2的等比数列,首项
是公比为2的等比数列,首项![]() ,
,
所以![]() ,则
,则![]() ;
;
(2)由![]() ,得
,得![]() ,
,
∵![]() ,
,![]() ,∴数列
,∴数列![]() 是等比数列,
是等比数列,
∴![]() ,
,
![]() 时,
时,![]() ,不等式左边
,不等式左边![]() ,右边
,右边![]() ,不等式成立;
,不等式成立;
![]() 时,
时,![]() ,
,
不等式![]() 即为
即为![]() ,
,
下面用数学归纳法证明:
(i)![]() 时,左边
时,左边![]() ,右边
,右边![]() ,左边
,左边![]() 右边,不等式成立,
右边,不等式成立,
(ii)假设![]() 时,不等式成立,即
时,不等式成立,即![]() ,
,
∵![]() ,∴
,∴![]()
则![]() 时,左边=
时,左边=![]() ,
,
由归纳假设左边![]()
![]() ,
,
下面只要证![]() ,即证
,即证![]() ,
,
再用数学归纳法证明![]() :
:
①![]() 时,不等式左边
时,不等式左边![]() ,右边
,右边![]() ,不等式成立,
,不等式成立,
②假设![]() (
(![]() )时不等式成立,即
)时不等式成立,即![]() ,
,
则![]() 时,
时,![]() ,不等式也成立,
,不等式也成立,
由①②得![]() 时,不等式
时,不等式![]() 成立,
成立,
∴![]() 时,不等式成立,
时,不等式成立,
由(i)(ii),原不等式对一切正整数![]() 都成立.
都成立.
综上,原不等式得证.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为F,直线l与C交于M,N两点.
的右焦点为F,直线l与C交于M,N两点.
(1)若l过点F,点M,N到直线y=2的距离分别为d1,d2,且![]() ,求l的方程;
,求l的方程;
(2)若点M的坐标为(0,1),直线m过点M交C于另一点N′,当直线l与m的斜率之和为2时,证明:直线NN′过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,共享单车在我国各城市迅猛发展,为人们的出行提供了便利,但也给城市的交通管理带来了一些困难,为掌握共享单车在![]() 省的发展情况,某调查机构从该省抽取了5个城市,并统计了共享单车的
省的发展情况,某调查机构从该省抽取了5个城市,并统计了共享单车的![]() 指标
指标![]() 和
和![]() 指标
指标![]() ,数据如下表所示:
,数据如下表所示:
城市1 | 城市2 | 城市3 | 城市4 | 城市5 | |
| 2 | 4 | 5 | 6 | 8 |
| 3 | 4 | 4 | 4 | 5 |
(1)试求![]() 与
与![]() 间的相关系数
间的相关系数![]() ,并说明
,并说明![]() 与
与![]() 是否具有较强的线性相关关系(若
是否具有较强的线性相关关系(若![]() ,则认为
,则认为![]() 与
与![]() 具有较强的线性相关关系,否则认为没有较强的线性相关关系).
具有较强的线性相关关系,否则认为没有较强的线性相关关系).
(2)建立![]() 关于
关于![]() 的回归方程,并预测当
的回归方程,并预测当![]() 指标为7时,
指标为7时,![]() 指标的估计值.
指标的估计值.
(3)若某城市的共享单车![]() 指标
指标![]() 在区间
在区间![]() 的右侧,则认为该城市共享单车数量过多,对城市的交通管理有较大的影响交通管理部门将进行治理,直至
的右侧,则认为该城市共享单车数量过多,对城市的交通管理有较大的影响交通管理部门将进行治理,直至![]() 指标
指标![]() 在区间
在区间![]() 内现已知
内现已知![]() 省某城市共享单车的
省某城市共享单车的![]() 指标为13,则该城市的交通管理部门是否需要进行治理?试说明理由.
指标为13,则该城市的交通管理部门是否需要进行治理?试说明理由.
参考公式:回归直线![]() 中斜率和截距的最小二乘估计分别为
中斜率和截距的最小二乘估计分别为
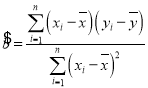 ,,
,,![]() 相关系数
相关系数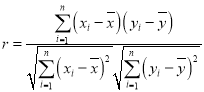
参考数据: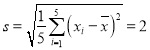 ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
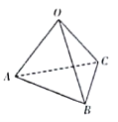
【题目】发展“会员”、提供优惠,成为不少实体店在网购冲击下吸引客流的重要方式.某连锁店为了吸引会员,在2019年春节期间推出一系列优惠促销活动.抽奖返现便是针对“白金卡会员”、“金卡会员”、“银卡会员”、“基本会员”不同级别的会员享受不同的优惠的一项活动:“白金卡会员”、“金卡会员”、“银卡会员”、“基本会员”分别有4次、3次、2次、1次抽奖机会.抽奖机如图:抽奖者第一次按下抽奖键,在正四面体的顶点![]() 出现一个小球,再次按下抽奖键,小球以相等的可能移向邻近的顶点之一,再次按下抽奖键,小球又以相等的可能移向邻近的顶点之一……每一个顶点上均有一个发光器,小球在某点时,该点等可能发红光或蓝光,若出现红光则获得2个单位现金,若出现蓝光则获得3个单位现金.
出现一个小球,再次按下抽奖键,小球以相等的可能移向邻近的顶点之一,再次按下抽奖键,小球又以相等的可能移向邻近的顶点之一……每一个顶点上均有一个发光器,小球在某点时,该点等可能发红光或蓝光,若出现红光则获得2个单位现金,若出现蓝光则获得3个单位现金.
(1)求“银卡会员”获得奖金的分布列;
(2)![]() 表示第
表示第![]() 次按下抽奖键,小球出现在
次按下抽奖键,小球出现在![]() 点处的概率.
点处的概率.
①求![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
②写出![]() 与
与![]() 关系式,并说明理由.
关系式,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直三棱柱ABC﹣A1B1C1中,平面ABC是下底面.M是BB1上的点,AB=3,BC=4,AC=5,CC1=7,过三点A、M、C1作截面,当截面周长最小时,截面将三棱柱分成的上、下两部分的体积比为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是2020年2月15日至3月2日武汉市新增新冠肺炎确诊病例的折线统计图.则下列说法不正确的是( )

A.2020年2月19日武汉市新增新冠肺炎确诊病例大幅下降至三位数
B.武汉市在新冠肺炎疫情防控中取得了阶段性的成果,但防控要求不能降低
C.2020年2月19日至3月2日武汉市新增新冠肺炎确诊病例低于400人的有8天
D.2020年2月15日到3月2日武汉市新增新冠肺炎确诊病例最多的一天比最少的一天多1549人
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在直角梯形![]() 中,
中,![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的点,
上的点,![]() ,且
,且![]() (如图①).将四边形
(如图①).将四边形![]() 沿
沿![]() 折起,连接
折起,连接![]() 、
、![]() 、
、![]() (如图②).在折起的过程中,则下列表述:
(如图②).在折起的过程中,则下列表述:

①![]() 平面
平面![]() ;
;
②四点![]() 、
、![]() 、
、![]() 、
、![]() 可能共面;
可能共面;
③若![]() ,则平面
,则平面![]() 平面
平面![]() ;
;
④平面![]() 与平面
与平面![]() 可能垂直.其中正确的是__________.
可能垂直.其中正确的是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)![]() sin(ωx+φ)﹣cos(ωx+φ)(0<φ<π,ω>0)为偶函数,且y=f(x)图象的两相邻对称轴间的距离为
sin(ωx+φ)﹣cos(ωx+φ)(0<φ<π,ω>0)为偶函数,且y=f(x)图象的两相邻对称轴间的距离为![]() ,则f(
,则f(![]() )的值为( )
)的值为( )
A.﹣1B.1C.![]() .D.
.D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com