
| 年份x | 2010 | 2011 | 2012 | 2013 | 2014 |
| 需求量y万吨 | 236 | 246 | 257 | 276 | 286 |
分析 (1)由所给数据看出,年需求量与年份之间是近似直线上升,利用回归直线方程,对数据预处理,求出预处理后的回归直线方程,从而求出对应的回归直线方程;
(2)利用所求的回归直线方程,计算2016年的粮食需求量即可.
解答 解:(1)由所给数据看出,年需求量与年份之间是近似直线上升,下面来求回归直线方程,先将数据预处理如下:
| 年份-2 012 | -2 | -1 | 0 | 1 | 2 |
| 需求量-257 | -21 | -11 | 0 | 19 | 29 |
点评 本题考查了求线性回归方程以及利用回归直线方程预测结果的应用问题,是基础题目.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
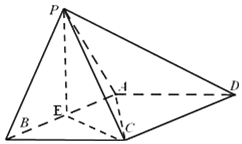 已知四棱锥P-ABCD,底面ABCD为菱形,∠ABC=60°,△PAB是等边三角形,AB=2,PC=$\sqrt{6}$,AB的中点为E
已知四棱锥P-ABCD,底面ABCD为菱形,∠ABC=60°,△PAB是等边三角形,AB=2,PC=$\sqrt{6}$,AB的中点为E查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a,b至少有一个为0 | B. | a,b至少有一个不为0 | ||
| C. | a,b全部为0 | D. | a,b中只有一个为0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{7}$ | C. | 3 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com