
���� ��С��90��Ľǿ����Ǹ��ǣ���һ���ǵ�һ���ǣ�
�ڽ�y=sin2x��ͼ�������е�ĺ���������ƽ��$\frac{��}{3}$����λ���ȣ��Ƕ�x�������ԣ�
�����������ǵ�һ���ǣ��Ҧ����£�����2��$+\frac{��}{6}$����$\frac{��}{3}$��
�ܸ������Һ����ĶԳ����жϼ��ɣ�
�ݸ��ݺ�����ͼ���жϼ��ɣ�
��� �⣺��С��90��Ľǿ���������һ���ޣ��ʴ����ǵ�һ���ǣ�
�ڽ�y=sin2x��ͼ�������е�����ƽ��$\frac{��}{3}$����λ���ȿɵõ�y=sin2��x-$\frac{��}{3}$����ͼ�ʴ���
�����������ǵ�һ���ǣ��Ҧ����£�������һ����ͬһ�������䣬��һ��sin����sin�£��ʴ���
�ܺ���f��$\frac{11��}{12}$��=-3���ʹ���ֱ��x=$\frac{11��}{12}$�Գƣ�����ȷ��
�ݸ��ݺ���y=|tanx|��ͼ����жϣ����������ںͶԳ��᷽�̷ֱ�Ϊ�У�x=$\frac{k��}{2}$��k��Z��������ȷ��
�ʴ�Ϊ���ܢݣ�
���� ���������Ǹ��ͼ���ƽ�ƣ����Ǻ����ĶԳ��Ժ����ڣ����ڻ���֪ʶ��Ӧ�������գ�


 ��У������Ԫͬ��ѵ��������ϵ�д�
��У������Ԫͬ��ѵ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
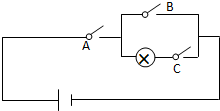 ��ͼ��ʾ��·����A��B��C�������أ�ÿ�����ؿ���صĸ��ʶ���$\frac{1}{2}$�������������������ĸ��ʣ�������
��ͼ��ʾ��·����A��B��C�������أ�ÿ�����ؿ���صĸ��ʶ���$\frac{1}{2}$�������������������ĸ��ʣ�������| A�� | $\frac{1}{8}$ | B�� | $\frac{1}{4}$ | C�� | $\frac{1}{2}$ | D�� | $\frac{1}{16}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com