Question

11．圆锥的母线与底面所成角为30°，高为2，则过圆锥顶点的平面截圆锥所得截面面积的最大值为8．

Answer 1

分析 求出圆锥的底面半径，假设截面与圆锥底面交于CD，CD=a，用a表示出截面三角形的高，得出截面三角形的面积关于a的表达式，利用基本不等式求出面积的最大值．

解答 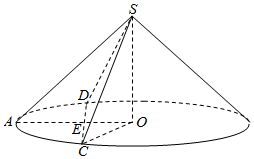解：∵圆锥的母线与底面所成角为30°，高为2，
∴圆锥的母线长l=4，底面半径r=2$\sqrt{3}$．
设过圆锥顶点的平面SCD与圆锥底面交于CD，过底面中心O作OA⊥CD于E，
设CD=a，则OE=$\sqrt{{r}^{2}-\frac{{a}^{2}}{4}}$=$\sqrt{12-\frac{{a}^{2}}{4}}$．（0＜a≤4$\sqrt{3}$）．
∴SE=$\sqrt{{h}^{2}+O{E}^{2}}$=$\sqrt{16-\frac{{a}^{2}}{4}}$．
∴截面SCD的面积S=$\frac{1}{2}$CD×SE=$\frac{1}{2}a$$\sqrt{16-\frac{{a}^{2}}{4}}$=$\sqrt{\frac{{a}^{2}}{4}（16-\frac{{a}^{2}}{4}）}$≤$\frac{16}{2}$=8．
故答案为：8．

点评 本题考查了圆锥的结构特征，基本不等式的应用，属于中档题．