
设二次函数 .
.
(1)求函数 的最小值;
的最小值;
(2)问是否存在这样的正数 ,当
,当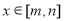 时,
时, ,且
,且 的值域为
的值域为 ?若存在,求出所有的
?若存在,求出所有的 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
(1)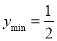 ;(2)
;(2)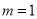 ,
,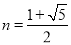 .
.
【解析】
试题分析:(1)这里遇到的是复合函数的最值问题,它是由简单的二次函数与指数函数复合而成的,遵循由内到外的解题顺序,很容易求出最小值;(2)这里是含参数的问题,常规方法是对参数分类讨论,如何分类,即分类的标准是什么?这是重点和难点,看解析往往是知其然,不知其所以然,这里的分类标准是将动区间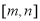 与二次函数
与二次函数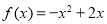 的定对称轴
的定对称轴 进行比较,自然就会分出它们有三种相对位置关系,即对称轴
进行比较,自然就会分出它们有三种相对位置关系,即对称轴 分别在区间
分别在区间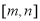 的左、中、右,故讨论分三种情形,当然讨论必须遵守不重不漏的原则,因此我们还必须关注细节,如区间的端点等,学会讨论重要,学会回避讨论更重要,它对化繁为简的能力要求非常高,这里的解法一是分类讨论的,而解法二就回避了讨论,解得很简洁,用心体会一下.
的左、中、右,故讨论分三种情形,当然讨论必须遵守不重不漏的原则,因此我们还必须关注细节,如区间的端点等,学会讨论重要,学会回避讨论更重要,它对化繁为简的能力要求非常高,这里的解法一是分类讨论的,而解法二就回避了讨论,解得很简洁,用心体会一下.
试题解析:(1)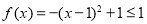 ,令
,令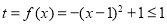
则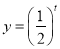 为
为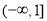 上减函数,因此,则当
上减函数,因此,则当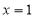 时,
时,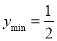 4分
4分
(2)法一:
①当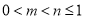 时,
时,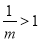
而当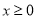 时,
时,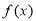 的最大值为
的最大值为 ,故此时不可能使
,故此时不可能使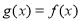 ,且
,且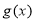 的值域为
的值域为 . 7分
. 7分
②当 时,
时,
则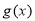 最大值为
最大值为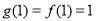 ,即
,即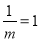 ,
,
得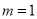 与
与 矛盾,故此时不可能. 10分
矛盾,故此时不可能. 10分
③当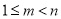 时,
时,
∵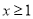 ,
,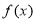 为减函数,则
为减函数,则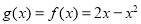
于是 ,即
,即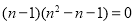 ,
,
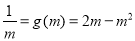
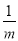 ,即
,即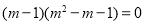
∵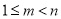 ,∴
,∴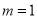 ,
,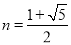 13分
13分
综上所述,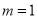 ,
,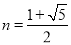 . 14分
. 14分
法二:
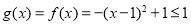 ,
,
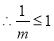 ,即
,即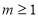 ,即
,即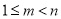 ,
,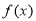 为
为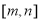 减函数,
减函数,
于是 ,即
,即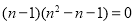 ,
,
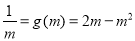
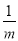 ,即
,即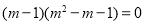
∵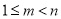 ,∴
,∴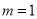 ,
,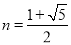 14分
14分
考点:1.函数性质的研究;2.含参数问题的讨论;3.函数、方程与不等式的综合.


科目:高中数学 来源:2015届广东省珠海市高三9月摸底考试文科数学试卷(解析版) 题型:选择题
若将一个质点随机投入如图所示的长方形ABCD中,其中AB=2,BC=1,则质点落在以AB为直径的半圆内的概率是( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届广东省高二下学期中段考文科数学试卷(解析版) 题型:选择题
记I为虚数集,设 ,
, ,
, 。则下列类比所得的结论正确的是( )
。则下列类比所得的结论正确的是( )
A.由 ,类比得
,类比得
B.由 ,类比得
,类比得
C.由 ,类比得
,类比得
D.由 ,类比得
,类比得
查看答案和解析>>
科目:高中数学 来源:2015届广东省高二下学期期末考试理科数学试卷(解析版) 题型:选择题
一个袋中装有大小相同的5个白球和3个红球,现在不放回的取2次球,每次取出一个球,记“第1次拿出的是白球”为事件 ,“第2次拿出的是白球”为事件
,“第2次拿出的是白球”为事件 ,则事件
,则事件 与
与 同时发生的概率是( )
同时发生的概率是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届广东省高二下学期期末考试文科数学试卷(解析版) 题型:解答题
设命题 :“若
:“若 ,则
,则 有实根”.
有实根”.
(1)试写出命题 的逆否命题;
的逆否命题;
(2)判断命题 的逆否命题的真假,并写出判断过程.
的逆否命题的真假,并写出判断过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com