
如图(1),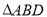 为等边三角形,
为等边三角形,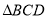 是以
是以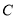 为直角顶点的等腰直角三角形且
为直角顶点的等腰直角三角形且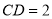 ,
,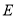 为线段
为线段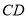 中点,将
中点,将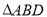 沿
沿 折起(如图2),使得线段
折起(如图2),使得线段 的长度等于
的长度等于 ,对于图二,完成以下各小题:
,对于图二,完成以下各小题:
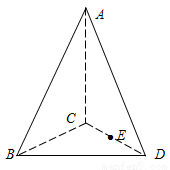
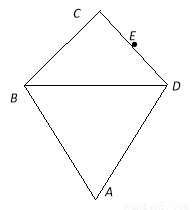
(图1) (图2)
(1)证明: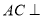 平面
平面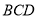 ;
;
(2)求直线 与平面
与平面 所成角的正弦值;
所成角的正弦值;
(3)线段 上是否存在点
上是否存在点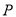 ,使得平面
,使得平面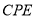 与平面
与平面 垂直?若存在,请求出线段
垂直?若存在,请求出线段 的长度;若不存在,请说明理由。
的长度;若不存在,请说明理由。
(1) 见解析
(2) 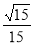
(3) 故线段AB上存在点P,此时线段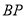 的长度为
的长度为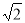
【解析】
试题分析:关于线面垂直的证明问题,注意把线面垂直的判定定理的内容记熟,对于线线、线面垂直的转化要熟悉,注意线面角的求法,并且第一步求出的直接结果就是线面角的正弦值,要看清要求的结果是谁,关于是否存在类问题,注意一般步骤,要先下结论,之后求解,能求出来就说明有,退出矛盾,就说明没有.
试题解析:(1)∵
又∵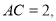 ∴
∴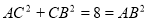 ∴
∴
同理可证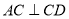 故
故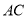 垂直面
垂直面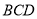 内两条相交直线
内两条相交直线
则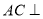 平面
平面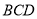 3分
3分
(2) 由(1)知 ,
,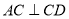 ,又有
,又有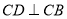
故可建如图所示建立空间直角坐标系C-xyz. 4分
∴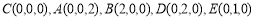
∴  ,
,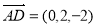 ,
,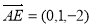 ,
,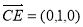
设平面ABD的一个法向量为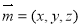 ,
,
则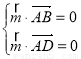
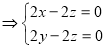 ,取
,取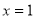 ,得
,得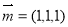 . 6分
. 6分
设直线AE与平面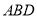 所成角为θ,
所成角为θ,
则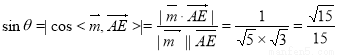 , 7分
, 7分
∴设直线AE与平面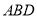 所成角的正弦值为
所成角的正弦值为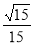 . 8分
. 8分
(3)假设存在符合条件的点P,并设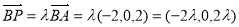 (
(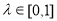 )
)
则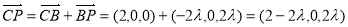
设平面CPE的一个法向量为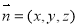 ,
,
则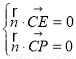
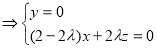 ,取
,取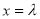 ,得
,得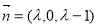 . 11分
. 11分
要使得平面CPE与平面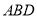 垂直,只需
垂直,只需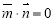 即
即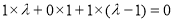
解得
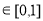 ,
,
故线段AB上存在点P,使得平面CPE与平面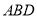 垂直,此时线段
垂直,此时线段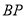 的长度为
的长度为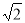 14分
14分
(说明:①答案提及“存在”而不能说明理由的得1分
②第(3)小题也可设P(2-t,0,t)展开解答)
考点:线面垂直,线面角,面面垂直.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2014-2015学年河北唐山市高三上学期期末考试文科数学试卷(解析版) 题型:选择题
设变量x、y满足 ,则目标函数
,则目标函数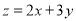 的最小值为( )
的最小值为( )
A.7 B.8 C.22 D.23
查看答案和解析>>
科目:高中数学 来源:2014-2015学年福建省高二上学期期末考试文科数学试卷(解析版) 题型:选择题
在平面直角坐标系中,曲线经过旋转或平移所产生的新双曲线与原双曲线具有相同的离心率和焦距,称它们为一组“任性双曲线”;例如将等轴双曲线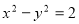 绕原点逆时针转动
绕原点逆时针转动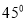 ,就会得到它的一条“任性双曲线”
,就会得到它的一条“任性双曲线”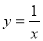 ;根据以上材料可推理得出双曲线
;根据以上材料可推理得出双曲线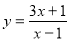 的焦距为( )
的焦距为( )
A.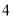 B.
B. 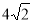 C.
C. 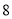 D.
D. 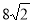
查看答案和解析>>
科目:高中数学 来源:2014-2015学年福建省高二上学期期末考试理科数学试卷(解析版) 题型:选择题
如果命题“若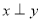 ,
,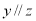 ,则
,则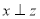 ”是假命题,那么字母
”是假命题,那么字母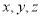 在空间所表示的几何图形可能是( )
在空间所表示的几何图形可能是( )
A. 全是直线 B.
全是直线 B. 全是平面
全是平面
C.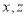 是直线,
是直线,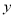 是平面 D.
是平面 D.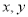 是平面,
是平面,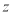 是直线
是直线
查看答案和解析>>
科目:高中数学 来源:2014-2015学年浙江省衢州市五校高三上学期期中联考文科数学试卷(解析版) 题型:填空题
在平面直角坐标系中, 分别是与
分别是与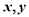 轴正方向同向的单位向量,平面内三点
轴正方向同向的单位向量,平面内三点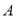 、
、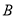 、
、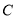 满足
满足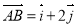 ,
, ,
,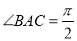 ,则实数m的值为 .
,则实数m的值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com