
| a |
| b |
| a |
| c |
| b |
| c |
| c |
科目:高中数学 来源: 题型:
| Sn |
| bn |
查看答案和解析>>
科目:高中数学 来源: 题型:
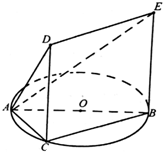 如图,已知五面体ABCDE,其中△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,且DC⊥平面ABC.
如图,已知五面体ABCDE,其中△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,且DC⊥平面ABC.查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 3 |
| 5 |
| 3 |
| F2M |
| F2N |
查看答案和解析>>
科目:高中数学 来源: 题型:
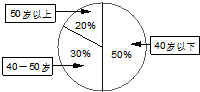 某单位200名职工的年龄分布情况如图示,该单位为了解职工每天的睡眠情况,按年龄用分层抽样方法从中抽取40名职工进行调查.则应从40-50岁的职工中抽取的人数为( )
某单位200名职工的年龄分布情况如图示,该单位为了解职工每天的睡眠情况,按年龄用分层抽样方法从中抽取40名职工进行调查.则应从40-50岁的职工中抽取的人数为( )| A、8 | B、12 | C、20 | D、30 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com