
分析 由题意画出图形,利用区域的面积比求概率.
解答 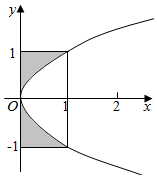 解:∵$\sqrt{{(x-\frac{1}{4})}^{2}{+y}^{2}}$≥|x+$\frac{1}{4}$|,
解:∵$\sqrt{{(x-\frac{1}{4})}^{2}{+y}^{2}}$≥|x+$\frac{1}{4}$|,
∴y2≥x,
平面区域D={(x,y)|0≤x≤1,|y|≤1},所围成图形为矩形,S矩形=1×2=2,
?(x,y)∈D,y2≥x,其面积为阴影部分的面积,其S阴影=${∫}_{-1}^{1}$y2dy=$\frac{1}{3}$y3|${\;}_{-1}^{1}$=$\frac{1}{3}$,
故?(x,y)∈D,$\sqrt{{(x-\frac{1}{4})}^{2}{+y}^{2}}$≥|x+$\frac{1}{4}$|的概率P=$\frac{{S}_{阴影}}{{S}_{矩形}}$=$\frac{1}{3}$,
故答案为:$\frac{1}{3}$
点评 本题考查了几何概型的概率求法;关键是明确事件的测度,利用公式解答.


科目:高中数学 来源: 题型:选择题
| A. | 3$\sqrt{13}$ | B. | 3$\sqrt{15}$ | C. | 3$\sqrt{21}$ | D. | 15 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x<-2或x>3} | B. | {x|x<-3或x>2} | C. | {x|-2<x<3} | D. | {x|-3<x<2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=$\frac{1}{f(x)}$ | B. | y=lg[1-f(x)] | C. | y=${\frac{1}{2}}^{f(x)}$ | D. | y=|f(x)| |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{AB}$+$\overrightarrow{BC}$=$\overrightarrow{AC}$ | B. | $\overrightarrow{AB}$+$\overrightarrow{AC}$=$\overrightarrow{BC}$ | C. | $\overrightarrow{AC}$+$\overrightarrow{BA}$=$\overrightarrow{AD}$ | D. | $\overrightarrow{AC}$+$\overrightarrow{AD}$=$\overrightarrow{DC}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com