
����Ŀ�����ں���![]() �����ǰ�ʹ
�����ǰ�ʹ![]() ��ʵ��
��ʵ��![]() ��������
��������![]() ����㣬����������
����㣬����������
����ڶ������������![]() ������
������![]() �ϵ�ͼ�����������ϵ�һ�����ߣ�������
�ϵ�ͼ�����������ϵ�һ�����ߣ�������![]() ����ô������
��������![]() ������
������![]() ������㣮�����������⣺
������㣮�����������⣺
��������![]() ��
��![]() ���ǵ�����������
���ǵ�����������![]() ��
��![]() �����ҽ���һ����㣻
�����ҽ���һ����㣻
������![]() ��
��![]() ����㣻
����㣻
������![]() ��
��![]() ��ͼ��Ľ�������ֻ��һ����
��ͼ��Ľ�������ֻ��һ����
���躯��![]() ��
��![]() ������
������![]() ���Һ���
���Һ���![]() ǡ��
ǡ��![]() ����ͬ����㣬����6�����ĺ�Ϊ18��
����ͬ����㣬����6�����ĺ�Ϊ18��
����������ȷ��������Ϊ________��(��������ȷ�������Ŷ�����)
���𰸡�����
������������![]() ��
��![]() ���ǵ�����������
���ǵ�����������![]() ��
��![]() �����ҽ���һ������Ǵ������������
�����ҽ���һ������Ǵ������������![]() ��
��![]() �ǵ������������亯��ֵ�����0������㣻
�ǵ������������亯��ֵ�����0������㣻
����![]() ��3�������ȷ������
��3�������ȷ������![]() ���ɽ�ú���
���ɽ�ú���![]() ������
������![]() ��
��![]() ��������������
��������������![]() �Ǽ��������ʺ������ڼ���ֵ
�Ǽ��������ʺ������ڼ���ֵ![]() ����Сֵ
����Сֵ![]() ���ʺ�����������㣻
���ʺ�����������㣻
����![]() ��
��![]() ͼ��Ľ�������ֻ��һ���Ǵ���ģ���Ϊ������ͼ��Ľ���ĺ�������Ǻ���
ͼ��Ľ�������ֻ��һ���Ǵ���ģ���Ϊ������ͼ��Ľ���ĺ�������Ǻ���![]() ����㣬
����㣬
����![]() ��������ֱ��
��������ֱ��![]() �Ҳ࣬������������㣮һ����
�Ҳ࣬������������㣮һ����![]() �ڣ�һ����
�ڣ�һ����![]() �ڣ��ʺ���
�ڣ��ʺ���![]()
����3����㣬������![]() ��
��![]() ��ͼ����3�����㣮
��ͼ����3�����㣮
���躯��![]() ��
��![]() ������
������![]() ���Һ���
���Һ���![]() ǡ��
ǡ��![]() ����ͬ����㣬����6�����ĺ�Ϊ18����ȷ�ģ��ɺ���
����ͬ����㣬����6�����ĺ�Ϊ18����ȷ�ģ��ɺ���![]() ��
��![]() ������
������![]() ���ɵú�����ͼ�����
���ɵú�����ͼ�����![]() �Գƣ��ֺ���
�Գƣ��ֺ���![]() ǡ��6����ͬ����㣬��6����㹹���������
ǡ��6����ͬ����㣬��6����㹹���������![]() �ԳƵĵ㣬���е����깫ʽ�ɵó���6�����ĺ�Ϊ18��
�ԳƵĵ㣬���е����깫ʽ�ɵó���6�����ĺ�Ϊ18��
�ʴ�Ϊ�ڢ�


 �����ҵ���������ϵ�д�
�����ҵ���������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѡ��4��4������ϵ��������̡�
��Բ![]() ��ÿһ��ĺ����걣�ֲ��䣬�������Ϊԭ����2����������C.
��ÿһ��ĺ����걣�ֲ��䣬�������Ϊԭ����2����������C.
����д��C�IJ������̣�
��������ֱ��![]() ��C�Ľ���Ϊ
��C�Ľ���Ϊ![]() ��������ԭ��Ϊ���㣬x��������Ϊ���Ὠ��������ϵ������߶�
��������ԭ��Ϊ���㣬x��������Ϊ���Ὠ��������ϵ������߶�![]() ���е�����
���е�����![]() ��ֱ��ֱ�ߵļ����귽��.
��ֱ��ֱ�ߵļ����귽��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ��� f (x) = x 2 + x��������ʽ f (��x) + f (x)��2 | x | �Ľ⼯ΪC. ��1����C ��2�������� f (a x)��a x + 1 = 5��a > 0��a��1���� C���н⣬��ʵ�� a ��ȡֵ��Χ�� ��3���� f (x) ��C �ϵ�ֵ��Ϊ A���� g(x) = x 3��3tx + ![]() ��x��[0,1] ��ֵ��ΪB���� A B����ʵ�� t ��ȡֵ��Χ.
��x��[0,1] ��ֵ��ΪB���� A B����ʵ�� t ��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=2x�� ![]() ��
��
��1����f��x��=2����x��ֵ��
��2����2tf��2t��+mf��t����0����t��[1��2]���������ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������![]() �У�
��![]() ����������
����������![]() ������
������![]() ��
��![]() . ��
. ��![]() �� ��ʹ��
�� ��ʹ��![]() ������
������![]() �����ֵΪ
�����ֵΪ![]() .
.
��1��������![]() Ϊ1��3��5��7��
Ϊ1��3��5��7��![]() ��д��
���![]() ��
��![]() ��
��![]() ��ֵ��
��ֵ��
��2����![]() Ϊ�Ȳ����У�������п��ܵ�����
Ϊ�Ȳ����У�������п��ܵ�����![]() ��
��
��3����![]() ��
��![]() ����
����![]() ��ֵ.����
��ֵ.����![]() ��ʾ��
��ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=Asin����x+�գ�+B��A��0���أ�0��|��|�� ![]() ������С������Ϊ2 �У���СֵΪ��2���ҵ�x=
������С������Ϊ2 �У���СֵΪ��2���ҵ�x= ![]() ʱ������ȡ�����ֵ4�� ��I������ f��x���Ľ���ʽ��
ʱ������ȡ�����ֵ4�� ��I������ f��x���Ľ���ʽ��
��������f��x���ĵ����������䣻
��������x��[ ![]() ��
�� ![]() ]ʱ������f��x��=m+1�н⣬��ʵ��m��ȡֵ��Χ��
]ʱ������f��x��=m+1�н⣬��ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����к����У�����f��x2��=[f��x��]2���ǣ� ��
A.f��x��=lnx
B.f��x��=|x+1|
C.f��x��=x3
D.f��x��=ex
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������P��ABCD�У�����ABCDΪ���Σ���ABC= ![]() ��PA�͵���ABCD��PA=AB=2��MΪPA���е㣬NΪBC���е�
��PA�͵���ABCD��PA=AB=2��MΪPA���е㣬NΪBC���е� 
��1��֤����ֱ��MN��ƽ��PCD��
��2��������ֱ��AB��MD���ɽǵ�����ֵ��
��3�����B��ƽ��PCD�ľ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪������ABC��A1B1C1�У�AB=5��AC=4��BC=3��AA1=4����D��AB�ϣ� 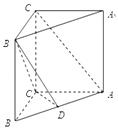
��1����D��AB�е㣬��֤��AC1��ƽ��B1CD��
��2���� ![]() =
= ![]() ʱ��������B��CD��B1������ֵ��
ʱ��������B��CD��B1������ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com