
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $-\frac{1}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
分析 由等比数列和等差数列的性质可知:a5=-2,b5=2π,$cos\frac{{{b_4}+{b_6}}}{{1-{a_3}•{a_7}}}$=cos$\frac{2{b}_{5}}{1-{a}_{5}^{2}}$=cos(-$\frac{4π}{3}$)=-$\frac{1}{2}$.
解答 解:由数列{an}是等比数列,由等比数列的性质可知:a1•a9=a3•a7=${a}_{5}^{2}$,
则a1•a5•a9=-8,即${a}_{5}^{3}$=-8,
∴a5=-2,
数列{bn}是等差数列,由等差数列的性质可知:b2+b8=4+b6=2b5,
b2+b5+b8=6π,即3b5=6π,
b5=2π,
∴$cos\frac{{{b_4}+{b_6}}}{{1-{a_3}•{a_7}}}$=cos$\frac{2{b}_{5}}{1-{a}_{5}^{2}}$=cos(-$\frac{4π}{3}$)=-cos$\frac{π}{3}$=-$\frac{1}{2}$,
故选C.
点评 本题考查等比数列及等差数列的性质,考查特殊角的三角形函数值,考查计算能力,属于中档题.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30 | B. | 31 | C. | 32 | D. | 33 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
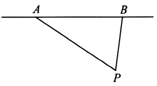 如图,在限速为90km/h的公路AB旁有一测速站P,已知点P距测速区起点A的距离为80m,距测速区终点B的距离为50m,且∠APB=60°.现测得某辆汽车从A点行驶到B点所用的时间为3s,则此车的速度介于( )
如图,在限速为90km/h的公路AB旁有一测速站P,已知点P距测速区起点A的距离为80m,距测速区终点B的距离为50m,且∠APB=60°.现测得某辆汽车从A点行驶到B点所用的时间为3s,则此车的速度介于( )| A. | 16~19m/s | B. | 19~22m/s | C. | 22~25m/s | D. | 25~28m/s |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com