
分析 (1)由对数换底公式得${log_{\sqrt{2}}}$7=2(log214-log22).结合已知即可得解.
(2)由诱导公式化简已知等式可得tan α=2.由直接代入法或同除转化法即可得解.
解答 本小题满分(12分),毎小问(6分).
解:(1)由对数换底公式得:${log_{\sqrt{2}}}7=\frac{{{{log}_2}7}}{{{{log}_2}\sqrt{2}}}=2{log_2}7=2({log_2}14-{log_2}2)$
=2($\frac{1}{a}-1$)=$\frac{2(1-a)}{a}$.…(6分)
(2)∵sin(3π+α)=2sin($\frac{3π}{2}$+α),
∴-sin α=-2cos α.…(2分)
∴sin α=2cos α,即tan α=2.…(3分)
方法一 (直接代入法):
原式=$\frac{2cosα-4cosα}{5×2cosα+2cosα}$=-$\frac{1}{6}$.…(6分)
方法二 (同除转化法):
原式=$\frac{tanα-4}{5tanα+2}$=$\frac{2-4}{5×2+2}$=-$\frac{1}{6}$.…(6分)
点评 本题主要考查了对数的运算,诱导公式的应用,属于基本知识的考查.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
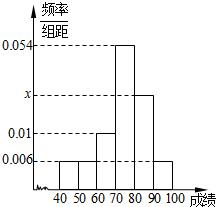 某班50位学生期中考试数学成绩的频率分布直方图如图所示.
某班50位学生期中考试数学成绩的频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{10}$) | B. | ($\frac{1}{10}$,1) | C. | (1,10) | D. | (10,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
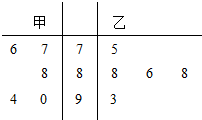 在“唱响内江”选拔赛中,甲、乙两位歌手的5次得分情况如茎叶图所示,记甲、乙两人的平均得分分别$\overline{{X}_{甲}}$、$\overline{{X}_{乙}}$,则下列判断正确的是( )
在“唱响内江”选拔赛中,甲、乙两位歌手的5次得分情况如茎叶图所示,记甲、乙两人的平均得分分别$\overline{{X}_{甲}}$、$\overline{{X}_{乙}}$,则下列判断正确的是( )| A. | $\overline{{X}_{甲}}$<$\overline{{X}_{乙}}$,乙比甲成绩稳定 | B. | $\overline{{X}_{甲}}$<$\overline{{X}_{乙}}$,甲比乙成绩稳定 | ||
| C. | $\overline{{X}_{甲}}$>$\overline{{X}_{乙}}$,甲比乙成绩稳定 | D. | $\overline{{X}_{甲}}$>$\overline{{X}_{乙}}$,乙比甲成绩稳定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com