
分析 分别以短轴两个顶点为直径的两个端点作圆O,以长轴两个顶点为直径的两个端点作圆O′,利用几何概型概率的计算公式,数形结合即得结论.
解答 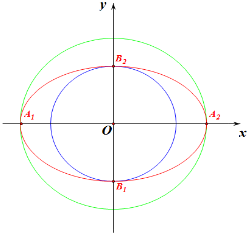 解:如图,以短轴两个顶点为直径的两个端点作圆O,
解:如图,以短轴两个顶点为直径的两个端点作圆O,
则圆O的面积为:πb2.
易得当点P位于圆O内(含边界)时,△PB1B2为钝角三角形,
∴△PB1B2为钝角三角形的概率为:$\frac{π{b}^{2}}{πab}$=$\frac{b}{a}$,
当点P位于圆O外、椭圆内(含边界)时,△PB1B2为锐角三角形,
∴△PB1B2为锐角三角形的概率为:1-$\frac{π{b}^{2}}{πab}$=1-$\frac{b}{a}$=$\frac{a-b}{a}$,
以长轴两个顶点为直径的两个端点作圆O′,
则在椭圆上或椭圆内部随机取一点P,△PA1A2为钝角三角形,
∴△PA1A2为钝角三角形的概率为1,
故答案为:①②④.
点评 本题以椭圆为载体,考查几何概型概率的计算,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 月份x | 1 | 2 | 3 | 4 | 5 |
| 用水量y | 2.5 | 3 | 4 | 4.5 | 5.2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | ±$\frac{1}{3}$ | C. | -$\frac{1}{3}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
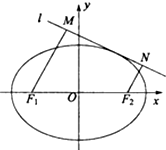 已知两点F1(-1,0),F2(1,0),点P在以F1,F2为焦点的椭圆C,且|PF1|,|F1F2|,|PF2|构成等差数列.
已知两点F1(-1,0),F2(1,0),点P在以F1,F2为焦点的椭圆C,且|PF1|,|F1F2|,|PF2|构成等差数列.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 48 | B. | 24 | C. | 36 | D. | 25 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com