
 下列命题:
下列命题:分析 ①作差与0比较,即可得到结论;
②求出三角形的高h=bsinA,与a比较即可.
③f(x)+f(1-x)=1,即可.
④根据等比数列的前n项和公式进行判断,
⑤以D为坐标原点,建立空间直角坐标系,利用向量的方法求出$\overrightarrow{DN}$与$\overrightarrow{{A}_{1}M}$夹角求出异面直线A1M与DN所成的角.
解答  解:①∵a,b,m都是正数,并且a<b,∴$\frac{a+m}{b+m}-\frac{a}{b}$=$\frac{m(b-a)}{b(b+m)}$>0,∴$\frac{a+m}{b+m}>\frac{a}{b}$,即①为真命题;
解:①∵a,b,m都是正数,并且a<b,∴$\frac{a+m}{b+m}-\frac{a}{b}$=$\frac{m(b-a)}{b(b+m)}$>0,∴$\frac{a+m}{b+m}>\frac{a}{b}$,即①为真命题;
②bsin60°=8×$\frac{\sqrt{3}}{2}$=4$\sqrt{3}$,
∵0<bsin60°<7,∴三角形有2解;故②错误
③若函数f(x)=$\frac{{4}^{x}}{{4}^{x}+2}$,
则f(x)+f(1-x)=$\frac{{4}^{x}}{{4}^{x}+2}$+$\frac{{4}^{1-x}}{{4}^{1-x}+2}$=$\frac{{4}^{x}}{{4}^{x}+2}$+$\frac{4}{4+2•{4}^{x}}$=$\frac{{4}^{x}}{{4}^{x}+2}$+$\frac{2}{2+{4}^{x}}$=$\frac{2+{4}^{x}}{2+{4}^{x}}$=1,
则f($\frac{1}{11}$)+f($\frac{2}{11}$)+f($\frac{3}{11}$)+…+f($\frac{10}{11}$)=5;成立,故③正确,
④在等比数列{an}中,当q≠1时,a1+a2+…+an=$\frac{{a}_{1}(1-{q}^{n})}{1-q}$(其中n∈N*,q为公比);
当q=1时,a1+a2+…+an=na1,故④错误,⑤以D为坐标原点,建立如图所示的空间直角坐标系.设棱长为2,
则D(0,0,0),N(0,2,1),M(0,1,0),A1(2,0,2),$\overrightarrow{DN}$=(0,2,1),$\overrightarrow{{A}_{1}M}$=(-2,1,-2)
$\overrightarrow{DN}$•$\overrightarrow{{A}_{1}M}$=0,所以$\overrightarrow{DN}$⊥$\overrightarrow{{A}_{1}M}$,即A1M⊥DN,异面直线A1M与DN所成的角的大小是90°,故⑤正确,
故答案为:①③⑤
点评 本题主要考查吗的真假判断,涉及的知识点较多,综合性较强,有一定的难度.


 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 赞同 | 反对 | 合计 | |
| 男 | 5 | 6 | 11 |
| 女 | 11 | 3 | 14 |
| 合计 | 16 | 9 | 25 |
| p(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
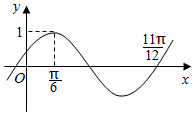 函数f(x)=Asin(ωx+φ)(A>0,ω>0)的图象如图所示,则以下步骤可以得到函数f(x)的图象的是( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0)的图象如图所示,则以下步骤可以得到函数f(x)的图象的是( )| A. | 将y=sinx的图象上的点纵坐标不变,横坐标变成原来的2倍,然后再向左平移$\frac{π}{6}$个单位 | |
| B. | 将y=sinx的图象上的点纵坐标不变,横坐标变成原来的2倍,然后再向右平移$\frac{π}{6}$个单位 | |
| C. | 将y=sinx的图象上的点纵坐标不变,横坐标变成原来的$\frac{1}{2}$,然后再向右平移$\frac{π}{12}$个单位 | |
| D. | 将y=sinx的图象上的点纵坐标不变,横坐标变成原来的$\frac{1}{2}$,然后再向左平移$\frac{π}{12}$个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{4}{9}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 大前提错误 | B. | 小前提错误 | ||
| C. | 推理形式错误 | D. | 大前提与推理形式都错误 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com