
分析 (Ⅰ)设出椭圆的标准方程,将A(1,$\frac{\sqrt{3}}{2}$)代入椭圆方程,利用离心率,构造方程组,从而求得椭圆C的标准方程.
(Ⅱ)设过点A(0,1)的直线l与椭圆C交于M(x1,y1),N(x2,y2),把直线代入椭圆的方程,再利用韦达定理求得 x1+x2 和x1•x2.根据OM⊥ON,即$\overrightarrow{OM}•\overrightarrow{ON}=0$,求得k的值.根可得直线l的方程.
解答 解:(Ⅰ)椭圆的方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$,(a>b>0),
∵椭圆C经过点A(1,$\frac{\sqrt{3}}{2}$),离心率为e=$\frac{\sqrt{3}}{2}$.
∴$\left\{\begin{array}{l}\frac{1}{{a}^{2}}+\frac{3}{{4b}^{2}}=1\\ \frac{{a}^{2}-{b}^{2}}{{a}^{2}}=\frac{3}{4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a}^{2}=4\\{b}^{2}=1\end{array}\right.$∴椭圆C的标准方程为$\frac{{x}^{2}}{4}+{y}^{2}=1$.
(Ⅱ)由题意知,直线l的斜率存在,过点B(-1,0)的直线l,y=k(x+1).
设直线l与椭圆C交于M(x1,y1),N(x2,y2)两点,
由$\left\{\begin{array}{l}\frac{{x}^{2}}{4}+{y}^{2}=1\\ y=kx+k\end{array}\right.$,可得 (4k2+1)x2+8k2x+4k2-4=0,
∴x1+x2=-$\frac{8{k}^{2}}{1+4{k}^{2}}$,x1•x2=$\frac{4{k}^{2}-4}{1+4{k}^{2}}$.
∵OM⊥ON,
∴$\overrightarrow{OM}•\overrightarrow{ON}=0$,
即 x1•x2+y1•y2=0,即(1+k2)x1•x2+k2(x1+x2)+k2=0,
即 (1+k2)($-\frac{8{k}^{2}}{1+4{k}^{2}}$)+k2(×$\frac{4{k}^{2}-4}{1+4{k}^{2}}$)+k2=0,解得k=±$\frac{\sqrt{21}}{7}$.
故直线l的方程为:y=±$\frac{\sqrt{21}}{7}$(x+1),即$\sqrt{21}$x-7y+$\sqrt{21}$=0,或$\sqrt{21}$x+7y-$\sqrt{21}$=0.
点评 本题主要考查椭圆的标准方程,直线和圆锥曲线的位置关系的Z综合应用,属于中档题.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 18种 | B. | 24种 | C. | 36种 | D. | 72种 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 在棱长为1的正方体ABCD-A1B1C1D1中,M是A1D1的中点,点P在侧面BCC1B1上运动.现有下列命题:
在棱长为1的正方体ABCD-A1B1C1D1中,M是A1D1的中点,点P在侧面BCC1B1上运动.现有下列命题:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 堵车时间(单位:小时) | 频数 |
| [0,1] | 8 |
| (1,2] | 6 |
| (2,3] | 38 |
| (3,4] | 24 |
| (4,5] | 24 |
| (表2) | |
| CD段 | EF段 | GH段 | |
| 堵车概率 | x | y | $\frac{1}{4}$ |
| 平均堵车时间 (单位:小时) | a | 2 | 1 |
| (表1) | |||
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
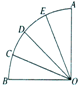 扇形AOB的半径为1,圆心角为90°,点C、D、E将弧AB分成四等分,连结OC、OD、OE,从图中所有的扇形中随机取出一个,面积恰好为$\frac{π}{8}$的概率是( )
扇形AOB的半径为1,圆心角为90°,点C、D、E将弧AB分成四等分,连结OC、OD、OE,从图中所有的扇形中随机取出一个,面积恰好为$\frac{π}{8}$的概率是( )| A. | $\frac{3}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com