
| 堵车时间(单位:小时) | 频数 |
| [0,1] | 8 |
| (1,2] | 6 |
| (2,3] | 38 |
| (3,4] | 24 |
| (4,5] | 24 |
| (表2) | |
| CD段 | EF段 | GH段 | |
| 堵车概率 | x | y | $\frac{1}{4}$ |
| 平均堵车时间 (单位:小时) | a | 2 | 1 |
| (表1) | |||
分析 (1)用每一段的时间的平均值乘以对应的概率,即为所求.
(2)先求出走线路甲所花汽油费的期望Eξ,再求出走乙线路多花汽油费的数学期望为Eη.择走甲线路应满足E(545+η)-Eξ≥0,结合x、y的范围,利用几何概型求出选择走甲线路的概率.
(4)用人数乘以选择走甲线路的概率,即为所求.
解答  解:(1)$a=0.5×\frac{8}{100}+1.5×\frac{6}{100}+2.5×\frac{38}{100}+3.5×\frac{24}{100}+4.5×\frac{24}{100}=3$.
解:(1)$a=0.5×\frac{8}{100}+1.5×\frac{6}{100}+2.5×\frac{38}{100}+3.5×\frac{24}{100}+4.5×\frac{24}{100}=3$.
(2)设走线路甲所花汽油费为ξ元,则Eξ=500(1-x)+(500+60)x=500+60x,
设走乙线路多花的汽油费为η元,∵EF段、GH段堵车与否相互独立,
∴$P(η=0)=(1-y)(1-\frac{1}{4})$,$P(η=20)=(1-y)\frac{1}{4}$,
$P(η=40)=y(1-\frac{1}{4})$,$P(η=60)=\frac{1}{4}y$,∴Eη=40y+5,
∴走乙线路所花汽油费的数学期望为E(545+η)=545+Eη=550+40y,
依题意选择走甲线路应满足(550+40y)-(500+60x)≥0,
$6x-4y-5≤0,又\frac{2}{3}<x<1,0<y<\frac{1}{2}$,
选择走甲线路的概率为图中阴影部分的面积与整个矩形面积之比,
即矩形的面积减去小直角三角形的面积的差除以矩形面积,
∴P(走路甲)=$\frac{7}{8}$,
(3)二项分布EX=4×$\frac{7}{8}$=3.5.
点评 本题主要考查离散型随机变量的分布列与数学期望,几何概型的应用,属于中档题.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
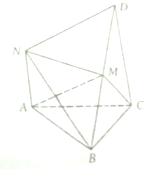 如图,在几何体NABCD中,CD⊥ABC.DC∥AN,CD=2AN=4,又AB=AC=BC=2,点M是BD上的动点(与B,D不重合)
如图,在几何体NABCD中,CD⊥ABC.DC∥AN,CD=2AN=4,又AB=AC=BC=2,点M是BD上的动点(与B,D不重合)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,△ABC为直角三角形,∠BAC=90°,PA⊥平面ABC,A为垂足.PC与底面成30°角,且AB=a,AC=2a.
如图,△ABC为直角三角形,∠BAC=90°,PA⊥平面ABC,A为垂足.PC与底面成30°角,且AB=a,AC=2a.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com