
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 求导分析分段函数在x≥0时的单调性,然后作出函数y=f(x)与y=$\frac{3}{4}$(x+1)的图象,数形结合得答案.
解答 解:当x≥0时,f(x)=x(x-2)2=x3-4x2+4x,f′(x)=3x2-8x+4=(3x-2)(x-2),
∴当x∈[$0,\frac{2}{3}$)∪(2,+∞)时,f′(x)>0,当x∈($\frac{2}{3},2$)时,f′(x)<0,
∴f(x)=x(x-2)2在[$0,\frac{2}{3}$),(2,+∞)上为增函数,在($\frac{2}{3},2$)上为减函数,
而f(0)=0,f($\frac{2}{3}$)=$\frac{32}{27}$,f(2)=0,当x→+∞时,f(x)→+∞;
函数y=f(x)-$\frac{3}{4}$(x+1)的零点,就是方程f(x)-$\frac{3}{4}$(x+1)=0的根,也就是两个函数y=f(x)与y=$\frac{3}{4}$(x+1)的图象交点的横坐标.
作出两个函数的图象如图,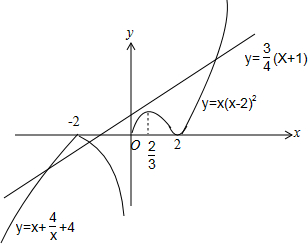
由图可知,函数y=f(x)-$\frac{3}{4}$(x+1)的零点个数为3个.
故选:B.
点评 本题考查函数零点判定定理,考查了利用导数一句话是的单调性,考查数形结合的解题思想方法,是中档题.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 至少有一个不小于2 | B. | 都小于2 | ||
| C. | 至少有一个不大于2 | D. | 都大于2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
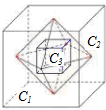 如图,记棱长为1的正方体C1,以C1各个面的中心为顶点的正八面体为C2,以C2各面的中心为顶点的正方体为C3,以C3各个面的中心为顶点的正八面体为C4,…,以此类推得一系列的多面体Cn,设Cn的棱长为an,则数列{an}的各项和为$\frac{6+3\sqrt{2}}{4}$.
如图,记棱长为1的正方体C1,以C1各个面的中心为顶点的正八面体为C2,以C2各面的中心为顶点的正方体为C3,以C3各个面的中心为顶点的正八面体为C4,…,以此类推得一系列的多面体Cn,设Cn的棱长为an,则数列{an}的各项和为$\frac{6+3\sqrt{2}}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x<0,$\frac{x}{x-1}$≤0 | B. | ?x>0,0≤x<1 | C. | ?x>0,$\frac{x}{x-1}$≤0 | D. | ?x<0,0≤x≤1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com