Question

已知△ABC的内角A、B、C成等差数列，且A、B、C所对的边分别为a、b、c，则下列命题中正确的有________(把所有正确的命题序号都填上)．

①B＝；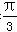                    

②若a、b、c成等比数列，则△ABC为等边三角形；

③若a＝2c，则△ABC为锐角三角形；   

④若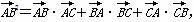则3A＝C；

⑤若tan A＋tan C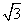＋＞0，则△ABC为钝角三角形．

Answer 1

①②④   

[解析]∵内角A、B、C成等差数列，∴A＋C＝2B．

又A＋B＋C＝π．∴B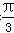＝，故①正确；

对于②，由余弦定理得b²＝a²＋c²－2ac·cos B＝a²＋c²－ac．

又b²＝ac，∴a²＋c²－ac＝ac，即(a－c)²＝0，∴a＝c，又B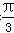＝，∴△ABC为等边三角形；

对于③，∵b²＝a²＋c²－2accos B＝4c²＋c²－2c²＝3c²，

∴b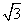＝c，此时满足a²＝b²＋c²，说明△ABC是直角三角形；

对于④，c²＝bccos A＋accos B＋abcos C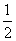＝ac＋b(ccos A＋acos C)

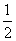＝ac＋b²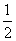＝ac＋a²＋c²－ac，化简得c＝2a，又b²＝a²＋c²－ac＝3a²，∴b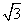＝a，

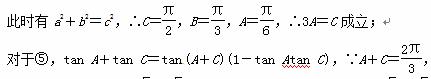∴tan A＋tan C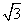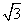＝－＋tan Atan C，∵tan A＋tan C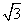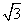＋＝tan Atan C＞0，

又在△ABC中，A、C不能同为钝角，∴A、C都是锐角，∴△ABC为锐角三角形．