
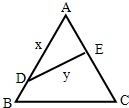
 如图,某公园有一块边长为2的等边△ABC的边角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.
如图,某公园有一块边长为2的等边△ABC的边角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.分析 (Ⅰ)在△ADE中,由余弦定理可得x,y,AE之间的关系,然后由S△ADE=$\frac{1}{2}$S△ABC,结合面积公式可求x与AE的关系,从而可求;
(Ⅱ)由题意可得y=$\sqrt{{x}^{2}+\frac{4}{{x}^{2}}-2}$,利用基本不等式可求函数的最小值.
解答 解:(Ⅰ)在△ADE中,y2=x2+AE2-2x•AE•cos60°⇒y2=x2+AE2-x•AE,①,
又S△ADE=$\frac{1}{2}$S△ABC=$\frac{\sqrt{3}}{2}$=$\frac{1}{2}$x•AE•sin60°②
∴AE=$\frac{2}{x}$≤2
∴x≥1,
②代入①得y2=x2+($\frac{2}{x}$)2-2(y>0)),
∴y=$\sqrt{{x}^{2}+\frac{4}{{x}^{2}}-2}$(1≤x≤2),
(Ⅱ)如果DE是水管y=$\sqrt{{x}^{2}+\frac{4}{{x}^{2}}-2}$≥$\sqrt{2•2-2}$=$\sqrt{2}$,
当且仅当x2=$\frac{4}{{x}^{2}}$,即x=$\sqrt{2}$时“=”成立,
故DE∥BC且AD=$\sqrt{2}$时水管的长度最短.
点评 本题主要考查了余弦定理,三角形的面积公式在求解三角形中的应用,及基本不等式在函数的最值求解中的应用,计算虽然简单,但是考查的内容具有较强的综合性.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
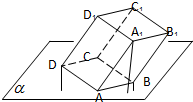 多面体上,位于同一条棱两端的顶点称为相邻的,如图,正方体的一个顶点A在平面α内,其余顶点在α的同侧,正方体上与顶点A相邻的三个顶点到α的距离分别为1,2和4,P是正方体的其余四个顶点中的一个,则P到平面α的距离可能是:(2)(4)(5)(6).(写出所有正确结论的编号)
多面体上,位于同一条棱两端的顶点称为相邻的,如图,正方体的一个顶点A在平面α内,其余顶点在α的同侧,正方体上与顶点A相邻的三个顶点到α的距离分别为1,2和4,P是正方体的其余四个顶点中的一个,则P到平面α的距离可能是:(2)(4)(5)(6).(写出所有正确结论的编号)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m?α,n?α,m∥n,则m∥α | B. | 若m⊥α,m?β,则α⊥β | ||
| C. | 若m?α,n?β,α∥β,则m∥n | D. | 若m⊥α,m⊥β,则α∥β |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com