
 某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩的茎叶图如图,其中甲班学生成绩的平均分是85,乙班学生成绩的中位数是83.
某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩的茎叶图如图,其中甲班学生成绩的平均分是85,乙班学生成绩的中位数是83.分析 (1)由甲班学生成绩的平均分是85,乙班学生成绩的中位数是83,利用茎叶图,列出方程组能求出x,y.
(2)由茎叶图能求出甲班学生的众数和乙班学生的众数.
(3)由甲班学生的平均数是85,能求出甲班7位学生成绩的方差.
解答 解:(1)∵甲班学生成绩的平均分是85,乙班学生成绩的中位数是83,
∴由茎叶图,得:
$\left\{\begin{array}{l}{\frac{1}{7}(78+79+80+80+x+85+92+96)=85}\\{80+y=83}\end{array}\right.$,
解得x=5,y=3.
(2)由茎叶图知,甲班学生的众数是85,
乙班学生的众数是81和91.
(3)∵甲班学生的平均数是85,
∴甲班7位学生成绩的方差:
S2=$\frac{1}{7}$[(78-85)2+(79-85)2+(80-85)2+(85-85)2+(85-85)2+(92-85)2+(96-85)2]=40.
点评 本题考查茎叶图的应用,考查众数、平均数、中位数、方差、茎叶图等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | y=cos(2x+$\frac{π}{4}$) | B. | y=cos($\frac{x}{2}$+$\frac{π}{4}$) | C. | y=sin2x | D. | y=-sin2x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
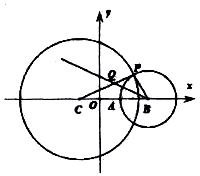 如图,在平面直角坐标系xoy中,已知圆C:(x+1)2+y2=16,点A(1,0),点B(a,0)(|a|>3),以B为圆心,|BA|的半径作圆,交圆C于点P,且的∠PBA的平分线次线段CP于点Q.
如图,在平面直角坐标系xoy中,已知圆C:(x+1)2+y2=16,点A(1,0),点B(a,0)(|a|>3),以B为圆心,|BA|的半径作圆,交圆C于点P,且的∠PBA的平分线次线段CP于点Q.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | -4$\sqrt{3}$ | C. | $\frac{4\sqrt{3}}{3}$ | D. | -$\frac{4\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com