
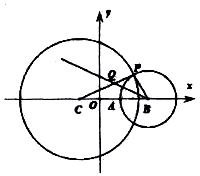
 如图,在平面直角坐标系xoy中,已知圆C:(x+1)2+y2=16,点A(1,0),点B(a,0)(|a|>3),以B为圆心,|BA|的半径作圆,交圆C于点P,且的∠PBA的平分线次线段CP于点Q.
如图,在平面直角坐标系xoy中,已知圆C:(x+1)2+y2=16,点A(1,0),点B(a,0)(|a|>3),以B为圆心,|BA|的半径作圆,交圆C于点P,且的∠PBA的平分线次线段CP于点Q.分析 (I)推导出△QAB≌△QPB,从而QC+QA=4,由椭圆的定义可知,Q点的轨迹是以C,A为焦点,2a=4的椭圆,由此能求出点Q的轨迹方程.
(II)设直线l:x=my-1,设M(x1,y1),N(x2,y2),推导出$\frac{S_2}{S_1}=\frac{{|{y_2}|}}{{|{y_1}|}}=-\frac{y_2}{y_1}$,由$\left\{\begin{array}{l}x=my-1\\ \frac{x^2}{4}+\frac{y^2}{3}=1\end{array}\right.$,得(3m2+4)y2-6my-9=0,由此利用根的判别式、韦达定理,结合已知条件求出$\frac{S_1}{S_2}$的取值范围.
解答 解:(I)如图,∵BA=BP,BQ=BQ,∠PBQ=∠ABQ,
∴△QAB≌△QPB,∴QA=QP,
∵CP=CQ+QP=QC+QA,QC+QA=4,
由椭圆的定义可知,Q点的轨迹是以C,A为焦点,2a=4的椭圆,
故点Q的轨迹方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$
(II)由题可知,设直线l:x=my-1,不妨设M(x1,y1),N(x2,y2)
∵${S_1}={S_{△OMC}}=\frac{1}{2}×|{OC}|×|{y_1}|,{S_2}={S_{△ONC}}=\frac{1}{2}×|{OC}|×|{y_2}|$,
$\frac{S_2}{S_1}=\frac{{|{y_2}|}}{{|{y_1}|}}=-\frac{y_2}{y_1}$,
∵$\left\{\begin{array}{l}x=my-1\\ \frac{x^2}{4}+\frac{y^2}{3}=1\end{array}\right.$,∴(3m2+4)y2-6my-9=0,△=144m2+144>0,
∴$\left\{\begin{array}{l}{y_1}+{y_2}=\frac{6m}{{3{m^2}+4}}\\{y_1}{y_2}=\frac{-9}{{3{m^2}+4}}\end{array}\right.$,
∵$\frac{{{{({y_1}+{y_2})}^2}}}{{{y_1}{y_2}}}=\frac{{-4{m^2}}}{{3{m^2}+4}}∈({-\frac{4}{3}}\right.,\left.0]$,
即$\frac{{y}_{1}}{{y}_{2}}+\frac{{y}_{2}}{{y}_{1}}+2$∈(-$\frac{4}{3}$,0],$\frac{{y}_{1}}{{y}_{2}}$∈(-3,-$\frac{1}{3}$),
∴$\frac{S_1}{S_2}$=-$\frac{{y}_{1}}{{y}_{2}}$∈($\frac{1}{3}$,3).
点评 本题考查点的轨迹方程的求法,考查两个三角形的面积的取值范围的求法,考查椭圆、韦达定理、根的判别式、直线方程、弦长公式等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,-3) | B. | (-1,3] | C. | (-∞,-3] | D. | (-3,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,e) | B. | (1,e) | C. | (e,2e) | D. | (e,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩的茎叶图如图,其中甲班学生成绩的平均分是85,乙班学生成绩的中位数是83.
某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩的茎叶图如图,其中甲班学生成绩的平均分是85,乙班学生成绩的中位数是83.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{11}{3}$ | B. | $\frac{13}{3}$ | C. | $\frac{14}{3}$ | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com