练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    4．不等式（a-3）x2+2（a-3）x-4＜0对于一切x∈R恒成立，那么a的取值范围是（　　）
    A．（-∞，-3）B．（-1，3]C．（-∞，-3]D．（-3，3]

    分析 当a=3时不等式即为-4＜0，对一切x∈R恒成立，当a≠3时 利用二次函数的性质列出a满足的条件并计算，最后两部分的合并即为所求范围．

    解答 解：当a-3=0，a=3时不等式即为-4＜0，对一切x∈R恒成立 ①
    当a≠3时，则须$\left\{\begin{array}{l}{a-3＜0}\\{△=4（a-3）^{2}+16（a-3）＜0}\end{array}\right.$，解得：$\left\{\begin{array}{l}{a＜3}\\{-1＜a＜3}\end{array}\right.$，
    ∴-1＜a＜3 ②
    由①②得实数a的取值范围是（-1，3]．
    故选：B．

    点评 本题考查不等式恒成立的参数取值范围，考查二次函数的性质．注意对二次项系数是否为0进行讨论．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    14．已知正方形的边长为1，$\overrightarrow{AB}=\overrightarrow a，\overrightarrow{BC}=\overrightarrow b，\overrightarrow{AC}=\overrightarrow c$，则$|{\overrightarrow a+\overrightarrow b+\overrightarrow c}|$等于（　　）
    A．0B．3C．$\sqrt{2}$D．$2\sqrt{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．在直角坐标系xOy中，曲线C1：$\left\{{\begin{array}{l}{x=3+αcost}\\{y=2+αsint}\end{array}}\right.$（t为参数，a＞0），在以坐标原点为极点，x轴的非负半轴为极轴的极坐标系中，曲线C2：ρ=4sinθ．
    （1）试将曲线C1与C2化为直角坐标系xOy中的普通方程，并指出两曲线有公共点时a的取值范围；
    （2）当a=3时，两曲线相交于A，B两点，求|AB|的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．设a=log0.80.9，b=log1.10.9，c=1.10.9，则a，b，c的大小关系为（　　）
    A．b＜a＜cB．a＜c＜bC．a＜b＜cD．c＜a＜b

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．将y=cosx的图象上的所有点的纵坐标不变，横坐标缩小到原来的一半，然后再将所得图象向左平移$\frac{π}{4}$个单位长度，则最后所得图象的解析式为（　　）
    A．y=cos（2x+$\frac{π}{4}$）B．y=cos（$\frac{x}{2}$+$\frac{π}{4}$）C．y=sin2xD．y=-sin2x

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．设函数$f（x）=\left\{\begin{array}{l}x-[x]，x≥0\\ f（x+1）\;，x＜0\end{array}\right.$其中[x]表示不超过x的最大整数如[-1.5]=-2，[2.5]=2，若直线y=k（x-1）（k＜0）与函数y=f（x）的图象只有三个不同的交点，则k的取值范围为（　　）
    A．$[-\frac{1}{2}，-\frac{1}{3}]$B．$（-\frac{1}{2}，-\frac{1}{3}）$C．$（-1，-\frac{1}{2}]$D．$（-1，-\frac{1}{2}）$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．要得到函数y=sin$\frac{1}{2}$x的图象，只需将函数y=sin（$\frac{1}{2}$x+$\frac{π}{6}$）的图象（　　）
    A．向左平移$\frac{π}{3}$个单位B．向右平移$\frac{π}{3}$个单位
    C．向左平移$\frac{π}{6}$个单位D．向右平移$\frac{π}{6}$个单位

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．已知a＞0，b＞0，且$\sqrt{3}$是3a与3b的等比中项，若$\frac{1}{a}$+$\frac{4}{b}$≥2m2+3m恒成立，则实数m的取值范围是[-3，$\frac{3}{2}$]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

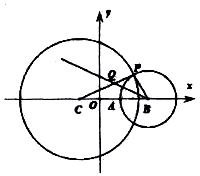    8．如图，在平面直角坐标系xoy中，已知圆C：（x+1）2+y2=16，点A（1，0），点B（a，0）（|a|＞3），以B为圆心，|BA|的半径作圆，交圆C于点P，且的∠PBA的平分线次线段CP于点Q．
    （I）当a变化时，点Q始终在某圆锥曲线τ是运动，求曲线τ的方程；
    （II）已知直线l过点C，且与曲线τ交于M、N两点，记△OCM面积为S1，△OCN面积为S2，求$\frac{S_1}{S_2}$的取值范围．

    查看答案和解析>>

    同步练习册答案