
| P��K2��k�� | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
���� ��1�������������е����ݣ�����K2��ֵ�����ɵõ����ۣ�
��2��X����ȡֵΪ0��1��2��3��X��B��3��$\frac{2}{3}$���������Ӧ�ĸ��ʣ��ɵ�X�ķֲ��м���ѧ������
��� �⣺��1�������������������̥��������Ϊ��
| ����̥ | ������̥ | �ϼ� | |
| 70�� | 30 | 15 | 45 |
| 80�� | 45 | 10 | 55 |
| �ϼ� | 75 | 25 | 100 |
| X | 0 | 1 | 2 | 3 |
| P | $\frac{1}{27}$ | $\frac{2}{9}$ | $\frac{4}{9}$ | $\frac{8}{27}$ |
���� ���⿼������Լ��飬������ɢ����������ķֲ���������������ѧ�����Ķ�����������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | g��x��Ϊ�溯�� | B�� | ����ֱ��$x=\frac{��}{2}$�Գ� | ||
| C�� | ���ڵ㣨�У�0���Գ� | D�� | ��$��-\frac{��}{6}��\frac{��}{4}��$�ϵ��� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
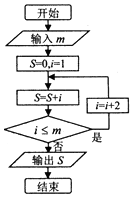
| A�� | 4 | B�� | 6 | C�� | 7 | D�� | 8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��0��1] | B�� | ��0��1�� | C�� | [1��2] | D�� | [0��1] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ijУij��N��ѧ����ѧ�����������ɼ�������120�֣���Ƶ�ʷֲ�ֱ��ͼ���£���֪������100-110��ѧ������21�ˣ�1����������N�ͷ�����110-115�ֵ�����n����
ijУij��N��ѧ����ѧ�����������ɼ�������120�֣���Ƶ�ʷֲ�ֱ��ͼ���£���֪������100-110��ѧ������21�ˣ�1����������N�ͷ�����110-115�ֵ�����n����| ��ѧ��x�� | 88 | 83 | 117 | 92 | 108 | 100 | 112 |
| ������y�� | 94 | 91 | 108 | 96 | 104 | 101 | 106 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | $\frac{1}{2e}$ | C�� | $\frac{1}{e}$ | D�� | $\frac{1}{{e}^{2}}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com