
分析 由对任意x∈R,不等式x2-2x-1≥m2-3m恒成立,运用二次函数的最值求法,可得m2-3m≤-2,解不等式可得m的范围,再由¬p为真命题时,则P为假命题,即可得到所求m的范围.
解答 解:∵对任意x∈R,不等式x2-2x-1≥m2-3m恒成立,
∴${[{{{({x-1})}^2}-2}]_{min}}≥{m^2}-3m$,即m2-3m≤-2,
即有(m-1)(m-2)≤0,
解得1≤m≤2.
因此,若¬p为真命题时,则P为假命题,
可得m的取值范围是(-∞,1)∪(2,+∞).
故答案为:(-∞,1)∪(2,+∞).
点评 本题考查不等式恒成立问题的解法,注意运用二次函数的最值求法和二次不等式的解法,同时考查命题的真假判断,考查转化和运算能力,属于中档题.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:选择题
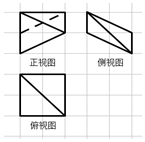 如图,网格纸上正方形小格的边长为1,图中粗线画出的是某几何体的三视图,则该几何体的体积为( )
如图,网格纸上正方形小格的边长为1,图中粗线画出的是某几何体的三视图,则该几何体的体积为( )| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{8}{3}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
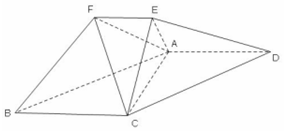 在如图所示的几何体中,平面ACE⊥平面ABCD,四边形ABCD 为平行四边形,
在如图所示的几何体中,平面ACE⊥平面ABCD,四边形ABCD 为平行四边形,查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x,y∈R,若x+y≠0,则x≠1且y≠-1 | |
| B. | a∈R,“$\frac{1}{a}<1$”是“a>1”的必要不充分条件 | |
| C. | 命题“?x∈R,使得x2+2x+3<0”的否定是“?x∈R,都有x2+2x+3>0” | |
| D. | 设随机变量X~N(1,52),若P(X<0)=P(X>a-2),则实数a的值为2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
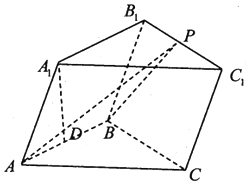 在三棱柱ABC-A1B1C1中,已知侧面ABB1A1是菱形,侧面BCC1B1是正方形,点A1在底面ABC的投影为AB的中点D.
在三棱柱ABC-A1B1C1中,已知侧面ABB1A1是菱形,侧面BCC1B1是正方形,点A1在底面ABC的投影为AB的中点D.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 14 | B. | 16 | C. | 36 | D. | 56 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com