
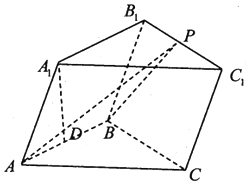
 在三棱柱ABC-A1B1C1中,已知侧面ABB1A1是菱形,侧面BCC1B1是正方形,点A1在底面ABC的投影为AB的中点D.
在三棱柱ABC-A1B1C1中,已知侧面ABB1A1是菱形,侧面BCC1B1是正方形,点A1在底面ABC的投影为AB的中点D.分析 (1)由点A1在底面ABC的投影为AB的中点D,可得A1D⊥平面ABC,则A1D⊥BC,再由已知可得B1B⊥BC,由线面垂直的判定可得BC⊥平面ABB1A1,从而得到平面AA1B1B⊥平面BB1C1C;
(2)以点D为坐标原点建立空间直角坐标系,设菱形边长为2,得到对应点的坐标,求出平面ABP与平面ABB1A1的法向量,由两法向量所成角的余弦值求得二面角A1-AB-P的正弦值.
解答 (1)证明:∵点A1在底面ABC的投影为AB的中点D,
∴A1D⊥平面ABC,则A1D⊥BC,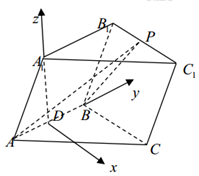
又∵侧面BCC1B1是正方形,∴B1B⊥BC,
∵B1B与A1D在平面ABB1A1上不平行,
∴BC⊥平面ABB1A1,
∴平面AA1B1B⊥平面BB1C1C;
(2)解:如图所示,以点D为坐标原点建立空间直角坐标系,
不妨设菱形边长为2,得D(0,0,0),A(0,-1,0),B(0,1,0),
∵D为AB的中点,且有A1D⊥AB,∴AA1=A1B,
又∵平面ABB1A1为菱形,∴△A1AB为等边三角形,
从而$∠{A_1}AD=\frac{π}{3}$,从而${A_1}D=2sin\frac{π}{3}=\sqrt{3}$,
∴点A1的坐标为$(0,0,\sqrt{3})$,
∵$\overrightarrow{{A_1}{B_1}}=\overrightarrow{AB}=(0,2,0)$,∴${B_1}(0,2,\sqrt{3})$,
又∵$\overrightarrow{{B_1}P}=\frac{1}{3}\overrightarrow{{B_1}{C_1}}=\frac{1}{3}\overrightarrow{BC}=(\frac{2}{3},0,0)$,∴$P(\frac{2}{3},2,\sqrt{3})$,
设平面ABP的法向量为$\overrightarrow{n_1}=(x,y,z)$,
由$\overrightarrow{BP}=(\frac{2}{3},1,\sqrt{3})$,$\overrightarrow{AB}=(0,2,0)$,
得$\left\{\begin{array}{l}\overrightarrow{n_1}•\overrightarrow{AP}=0\\ \overrightarrow{n_1}•\overrightarrow{AB}=0\end{array}\right.$,即$\left\{\begin{array}{l}\frac{2}{3}x+y+\sqrt{3}z=0\\ 2y=0\end{array}\right.$,
令$x=\sqrt{3}$,则$z=-\frac{2}{3}$,y=0,∴$\overrightarrow{n_1}=(\sqrt{3},0,-\frac{2}{3})$,
同理求得平面ABB1A1的法向量$\overrightarrow{n_2}=(1,0,0)$,
∴$cos<\overrightarrow{n_1},\overrightarrow{n_2}>=\frac{{\overrightarrow{n_1}•\overrightarrow{n_2}}}{{|\overrightarrow{n_1}|•|\overrightarrow{n_2}|}}=\frac{{\sqrt{3}}}{{\sqrt{\frac{31}{9}}}}=\frac{{3\sqrt{93}}}{31}$,
∴$sin<\overrightarrow{n_1},\overrightarrow{n_2}>=\frac{{2\sqrt{31}}}{31}$,
从而二面角A1-AB-P的正弦值为$\frac{{2\sqrt{31}}}{31}$.
点评 本题考查面面垂直的判定,考查利用空间向量求二面角的平面角,考查空间想象能力和思维能力,属中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(1,\frac{{\sqrt{6}}}{2}]$ | B. | $[\frac{{\sqrt{6}}}{2},+∞)$ | C. | $(1,\frac{{\sqrt{6}}}{2})$ | D. | $(\frac{{\sqrt{6}}}{2},+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某校某次N名学生的学科能力测评成绩(满分120分)的频率分布直方图如下,已知分数在100-110的学生数有21人(1)求总人数N和分数在110-115分的人数n.;
某校某次N名学生的学科能力测评成绩(满分120分)的频率分布直方图如下,已知分数在100-110的学生数有21人(1)求总人数N和分数在110-115分的人数n.;| 数学(x) | 88 | 83 | 117 | 92 | 108 | 100 | 112 |
| 物理(y) | 94 | 91 | 108 | 96 | 104 | 101 | 106 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com