
分析 (1)求出f(x)的导数和切线的斜率,以及f(2),运用点斜式方程,可得切线的方程;
(2)求出G(x)的解析式,求出导数,再求导数,判断G′(x)的单调性,由零点存在定理可得存在唯一x0∈(1,2),使$G'({x_0})={e^{x_0}}-\frac{1}{x_0}-2=0$,即${e^{x_0}}=\frac{1}{x_0}+2$,构造$H(x)=\frac{1}{x}+2-lnx-2x$,(1<x<2),求出导数,判断单调性,即可得证.
解答 解:(1)$f'(x)=\frac{{{e^x}x-{e^x}}}{x^2}$,$f'(2)=\frac{{2{e^2}-{e^2}}}{2^2}=\frac{e^2}{4}$且$f(2)=\frac{e^2}{2}$,
所以切线方程$y-\frac{e^2}{2}=\frac{e^2}{4}(x-2)$,即$y=\frac{e^2}{4}x$.
(2)证明:由G(x)=xf(x)-lnx-2x(x>0),
$G'(x)={e^x}-\frac{1}{x}-2$.$G''(x)={e^x}+\frac{1}{x^2}>0$,所以G'(x)在(0,+∞)为增函数,
又因为G'(1)=e-3<0,$G'(2)={e^2}-\frac{5}{2}>0$,
所以存在唯一x0∈(1,2),使$G'({x_0})={e^{x_0}}-\frac{1}{x_0}-2=0$,
即${e^{x_0}}=\frac{1}{x_0}+2$,且当x∈(0,x0)时,G'(x)<0,G(x)为减函数,
x∈(x0,+∞)时G'(x)>0,G(x)为增函数,
所以$G{(x)_{min}}=G({x_0})={e^{x_0}}-ln{x_0}-2{x_0}=\frac{1}{x_0}+2-ln{x_0}-2{x_0}$,x0∈(1,2),
记$H(x)=\frac{1}{x}+2-lnx-2x$,(1<x<2),$H'(x)=-\frac{1}{x^2}-\frac{1}{x}-2<0$,
所以H(x)在(1,2)上为减函数,
所以$H(x)>H(2)=\frac{1}{2}+2-ln2-4=-\frac{3}{2}-ln2$,
所以$G(x)≥G({x_0})>-\frac{3}{2}-ln2$.
点评 本题考查导数的运用:求切线的方程和单调区间,注意运用导数的几何意义和函数的单调性,考查构造函数法,以及化简整理的运算能力,属于中档题.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
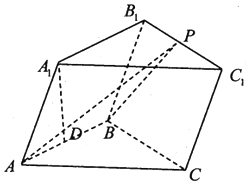 在三棱柱ABC-A1B1C1中,已知侧面ABB1A1是菱形,侧面BCC1B1是正方形,点A1在底面ABC的投影为AB的中点D.
在三棱柱ABC-A1B1C1中,已知侧面ABB1A1是菱形,侧面BCC1B1是正方形,点A1在底面ABC的投影为AB的中点D.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{2}$ | B. | $\frac{{3\sqrt{2}}}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{5}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{4}{7}$ | C. | $\frac{5}{7}$ | D. | $\frac{5}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{3}$ | B. | $\frac{5}{3}$ | C. | $\frac{7}{5}$ | D. | $\frac{8}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com