
分析 (1)当q=1,d=2时,an+1-an=2,从而数列{an}是首项a1=4,公差d=2的等差数列,由此能求出a2017.
(2)当q=3,d=-2时,an+1=3an-2变形得an+1-1=3(an-1),从而数列{an-1}是以3为首项,3为公比的等比数列,进而数列{bn}是以$\frac{1}{3}$为首项,$\frac{1}{3}$为公比的等比数列,由此能证明${S_n}<\frac{1}{2}$.
解答 (1)解:∵数列{an}满足a1=4,an+1=qan+d(q,d为常数).
∴当q=1,d=2时,an+1-an=2,
∴数列{an}是首项a1=4,公差d=2的等差数列,
∴an=4+(n-1)×2=2n+2,
∴a2017=2×2017+2=4036.
(2)证明:当q=3,d=-2时,an+1=3an-2变形得an+1-1=3(an-1)
∴数列{an-1}是以3为首项,3为公比的等比数列,
∴${a_n}-1=3×{3^{n-1}}={3^n}$,∴${b_n}=\frac{1}{{{a_n}-1}}={(\frac{1}{3})^n}$,
∴数列{bn}是以$\frac{1}{3}$为首项,$\frac{1}{3}$为公比的等比数列,
∴${S_n}={b_1}+{b_2}+{b_3}+…+{b_n}=\frac{{\frac{1}{3}(1-\frac{1}{3^n})}}{{1-\frac{1}{3}}}=\frac{1}{2}(1-\frac{1}{3^n})<\frac{1}{2}$,
∴${S_n}<\frac{1}{2}$.
点评 本题考查数列的第2017项的求法,考查数列的前n项和小于$\frac{1}{2}$的证明,是中档题,解题时要认真审题,注意等差数列、等比数列的性质的合理运用.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某校某次N名学生的学科能力测评成绩(满分120分)的频率分布直方图如下,已知分数在100-110的学生数有21人(1)求总人数N和分数在110-115分的人数n.;
某校某次N名学生的学科能力测评成绩(满分120分)的频率分布直方图如下,已知分数在100-110的学生数有21人(1)求总人数N和分数在110-115分的人数n.;| 数学(x) | 88 | 83 | 117 | 92 | 108 | 100 | 112 |
| 物理(y) | 94 | 91 | 108 | 96 | 104 | 101 | 106 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
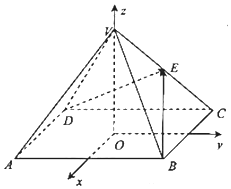 如图,以正四棱锥V-ABCD的底面中心O为坐标原点建立空间直角坐标系O-xyz,其中Ox∥BC,Oy∥AB,E为VC中点,正四棱锥的底面边长为2a,高为h,且有cos<$\overrightarrow{BE}$,$\overrightarrow{DE}$>=-$\frac{15}{49}$.
如图,以正四棱锥V-ABCD的底面中心O为坐标原点建立空间直角坐标系O-xyz,其中Ox∥BC,Oy∥AB,E为VC中点,正四棱锥的底面边长为2a,高为h,且有cos<$\overrightarrow{BE}$,$\overrightarrow{DE}$>=-$\frac{15}{49}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{2e}$ | C. | $\frac{1}{e}$ | D. | $\frac{1}{{e}^{2}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com